Пусть на вероятностном пространстве 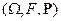 задана последовательность случайных величин
задана последовательность случайных величин 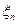 ,
, 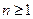 .
.
1. Последовательность случайных величин 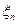 сходится к
сходится к 
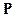 -п.н., если
-п.н., если 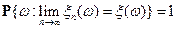 .
.
2. Последовательность 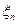 сходится к
сходится к  по вероятности (
по вероятности (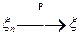 ), если для любого
), если для любого 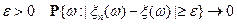 при
при 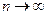 .
.
3. Последовательность 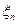 сходится к
сходится к  при
при 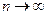 в
в 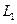
(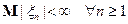 ), если
), если 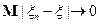 при
при 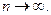
4. Последовательность 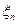 сходится к
сходится к  при
при 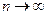 в
в 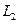
(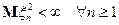 ), если
), если 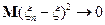 при
при 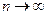 ; принято обозначение для такой сходимости
; принято обозначение для такой сходимости 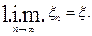
5. Последовательность 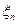 сходится по распределению (слабо сходится) к
сходится по распределению (слабо сходится) к  при
при 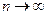 :
: 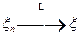 (
(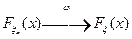 ), если для любой непрерывной ограниченной функции
), если для любой непрерывной ограниченной функции 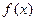
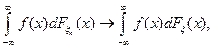
где 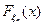 – функция распределения случайных величин
– функция распределения случайных величин 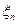 ,
, 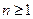 ,
, 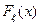 – функция распределения случайной величины
– функция распределения случайной величины  .
.
 2014-02-12
2014-02-12 546
546








