1. Из сходимости 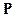 -п.н. следует сходимость по вероятности.
-п.н. следует сходимость по вероятности.
Доказательство. Предположим противное. Пусть 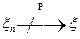 , т.е.
, т.е. 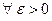 такого, что
такого, что 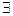
подпоследовательность 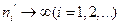 и
и 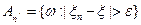 такие, что
такие, что 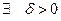 и
и 
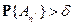 и
и 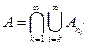 .
.
Заметим, что 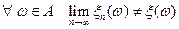 в силу того, что
в силу того, что 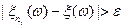 для бесконечного числа номеров
для бесконечного числа номеров 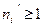 .
. 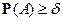 , так как
, так как 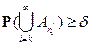 и
и 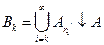 , т.е.
, т.е. 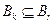 при
при 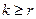 . Следовательно,
. Следовательно, 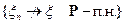 .
.
2. Пусть 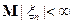 и
и 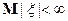 , тогда из сходимости в
, тогда из сходимости в 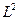 следует сходимость в
следует сходимость в 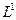 . Это следует из неравенства
. Это следует из неравенства 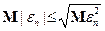 , где
, где 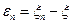 .
.
Аналогично из сходимости в 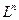 следует сходимость в
следует сходимость в 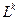 при
при 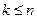 .
.
3. Из сходимости в 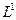 следует сходимость по вероятности.
следует сходимость по вероятности.
Доказательство. Из неравенства Чебышева следует, что 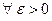

4. Пусть 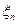 сходятся по вероятности к
сходятся по вероятности к  ,
, 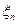 и
и  - равномерно ограничены (т.е.
- равномерно ограничены (т.е. 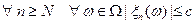 ). Тогда
). Тогда 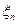 сходится к
сходится к  в
в 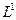 .
.
Доказательство. Рассмотрим функции 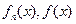 , такие, что
, такие, что 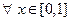 ,
, 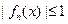 и
и 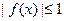 . Предположим, что
. Предположим, что 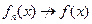 в
в 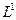 , т.е.
, т.е. 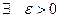 и
и 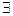 подпоследовательность
подпоследовательность 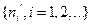 такие, что
такие, что

Обозначим 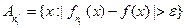 .
.
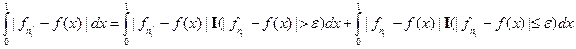 .
.
Заметим, что 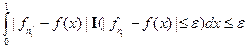 ; следовательно,
; следовательно, 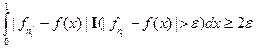 . Но
. Но 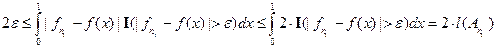 , значит
, значит 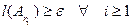 , т.е.
, т.е. 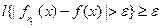 , и, следовательно,
, и, следовательно, 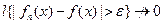 .
.
5. Пусть 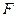 – функция распределения константы
– функция распределения константы 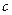 (
(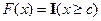 ), и последовательность
), и последовательность 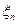 слабо сходится к
слабо сходится к 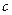 . Тогда
. Тогда 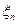 сходится к
сходится к 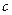 по вероятности.
по вероятности.
 2014-02-12
2014-02-12 374
374







