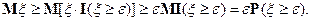
Доказательство свойства 12). Обозначим
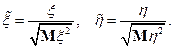
Доказательство проводим аналогично дискретному случаю.
Доказательство свойства 13). 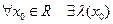 такое, что
такое, что 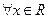 выполняется неравенство
выполняется неравенство
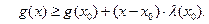
Возьмем 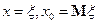 , тогда получим
, тогда получим
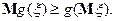
Доказательство свойства 14). 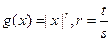 . Применим неравенство Йенсена к
. Применим неравенство Йенсена к 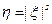 .
.
Доказательство свойства 15) следует из свойства 14).
Доказательство свойства 16). Делаем замену
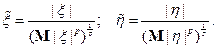
Применяем неравенство
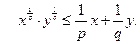
Для абсолютно-непрерывных распределений
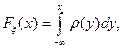
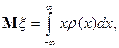
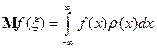
(можно предполагать, что 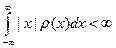 , и, соответственно,
, и, соответственно, 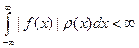 ).
).
Пусть  и
и 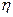 имеют совместное распределение
имеют совместное распределение 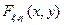 с плотностью
с плотностью 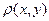
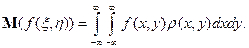
Если  и
и 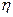 независимы, то
независимы, то 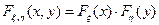 и
и 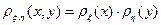 .
.
Пусть 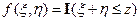 . Тогда
. Тогда
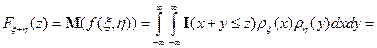
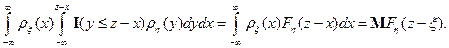
Т.е. для 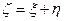 справедлива формула свертки
справедлива формула свертки
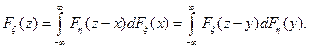
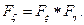
Аналогично
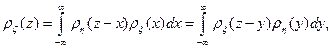
и аналогично 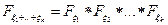 .
.
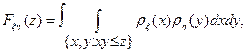
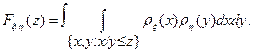
При 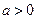
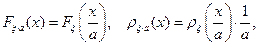
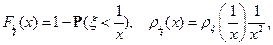
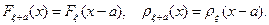
Пример. Пусть 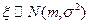 . Тогда
. Тогда 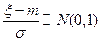 .
.
5. Характеристические функции
Определение. Характеристической функцией 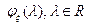 случайной величины
случайной величины  называют
называют
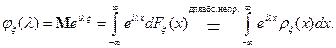
Т.е. для абсолютно непрерывных функций распределения 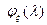 – преобразование Фурье
– преобразование Фурье 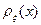 .
.
Характеристическая функция существует для любой случайной величины  , так как
, так как
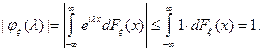
Свойства:
1) 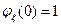 ,
, 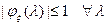
2) 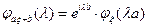
3) если 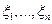 – независимы, то
– независимы, то 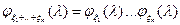
4) 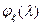 – равномерно по
– равномерно по 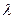 непрерывная функция
непрерывная функция
5) Если 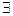
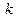 -й момент
-й момент 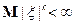 ,
, 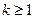 , то
, то 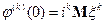
6) Если 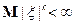 , то в окрестности точки
, то в окрестности точки 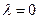
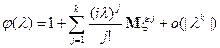
7) Если 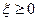 , то
, то 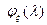 определена при комплексных
определена при комплексных 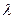 при
при 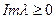 , и аналитична при
, и аналитична при 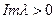 и непрерывна включая
и непрерывна включая 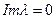
8) 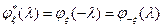 , где * – комплексное сопряжение, т.е., если
, где * – комплексное сопряжение, т.е., если 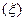 и
и 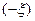 одинаково распределены, то характеристическая функция вещественна
одинаково распределены, то характеристическая функция вещественна
9) Если  имеет плотность, то
имеет плотность, то 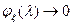 при
при 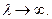
Доказательства свойств 1), 2), 3), 7), 8), 9) очевидны.
Доказательство свойства 4).
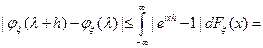
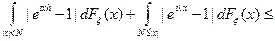
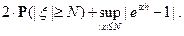
Выбираем 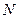 , а затем
, а затем 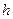 .
.
Доказательство свойства 5) следует из дифференцирования по 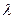 под знаком интеграла
под знаком интеграла
Доказательство свойства 6) следует из 5)
Формулы обращения (обратное преобразование Фурье).
Если 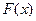 – функция распределения
– функция распределения  ,
, 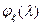 – характеристическая функция, то для любых точек непрерывности
– характеристическая функция, то для любых точек непрерывности 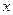 и
и 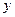
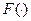
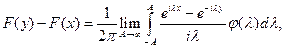
и если 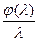 интегрируема, то
интегрируема, то
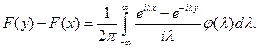
Если 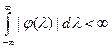 , то существует плотность
, то существует плотность 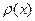 такая, что
такая, что
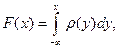
 2014-02-12
2014-02-12 367
367








