Геометрические операции над моделями

Современные системы компьютерной графики работают не только с плоскими изображениями, но и с объемными (трехмерными). Для выполнения преобразований в трех измерениях естественно распространить матричные операции и на трехмерные геометрические объекты. Для этого по аналогии с двухмерным случаем введем понятие однородных координат точки в пространстве. Заменим тройку чисел (x, y, z) четверкой (x, y, z, 1). В общем виде однородные координаты представляются в виде .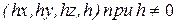

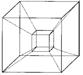
Рис. 5.4 – Куб и гиперкуб.

Как представить себе смысл величины h? По аналогии с двухмерным случаем h есть расстояние от координатного пространства XYZ до проективной гиперплоскости, на которую это пространство проектируется. Размерность гиперплоскости равна четырем. Мысленно представить себе четырехмерный объект практически невозможно (Рис. 5.4). Например, каждой гранью четырехмерного гиперкуба является привычный нам трехмерный куб и т.д.

Зададим элементарные операции в пространстве в виде матриц.

Матрица вращения вокруг оси абсцисс на угол :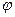

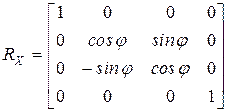
Следует помнить, что матрица соответствует линейной системе уравнений координат точек.

Матрица вращения вокруг оси ординат на угол :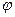

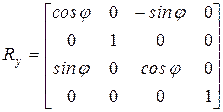
Матрица вращения вокруг оси аппликат на угол :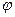

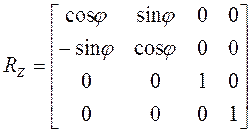
Очень важное свойство вращения в пространстве состоит в том, что оно некоммутативно. Коммутативностью называется независимость результата операции от порядка следования операндов. Например, для обычных чисел A×B=B×A. Для матриц же такое правило не соблюдается: при умножении матриц в общем случае A×B¹B×A. И действительно, результат вращения тела в пространстве зависит от последовательности выполнения вращений. Отметим, что вращение на плоскости вcегда коммутативно. Мы можем сначала повернуть объект на 15^о, а затем на 30^о, или наоборот – сначала на 30^о, а затем на 15^о – в обоих случаях тело окажется повернутым на 45^о.

Матрица масштабирования с коэффициентами сжатия/растяжения 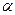вдоль оси абсцисс, 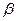- оси ординат, 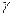- оси аппликат:

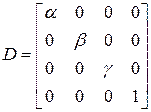
Для определения переноса объекта удобно воспользоваться вектором переноса с координатами 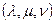, вдоль которого объект и перемещается в направлении вектора. Тогда можно записать следующую матрицу переноса:

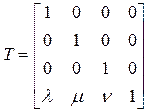
6. виды геометрических моделей их свойства,
параметризация моделей

Системы 3D моделирования должны тем или иным образом математически представлять трехмерные поверхности, из которых образуются моделируемые тела.