Поверхностная модель объекта определяется с помощью точек, линий и поверхностей. Метод поверхностного моделирования наиболее эффективен при проектировании и изготовлении сложных криволинейных поверхностей, таких, как корпуса автомобилей.
Существуют следующие основные типы поверхностей
1. Базовые геометрические поверхности. К ним относятся плоские поверхности, которые можно получить, начертив сначала отрезок прямой, а затем введя такую команду, которая разворачивает в трехмерном пространстве образ этого отрезка на заданное расстояние. Подобным образом (разверткой окружностей или дуг) могут быть сгенерированы цилиндрические и конические поверхности (Рис. 6.1).
Области поверхностей также могут быть развернуты в трехмерные объекты (Рис. 6.2). Следует отметить, что системы поверхностного моделирования не распознают такие формы, как твердые объемные тела; они представляют их просто как поверхности (на Рис. 6.2 семь плоских граней), соединенные друг с другом неким образом в пространстве и ограничивающие "пустой" объем.
|
|
|
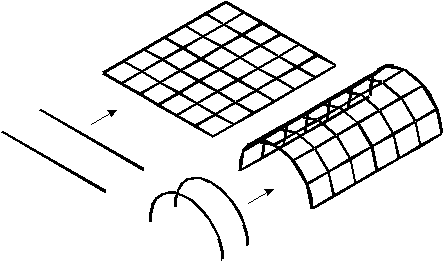
Рис. 6.1 – Формирование развернутых плоских и криволинейных поверхностей.
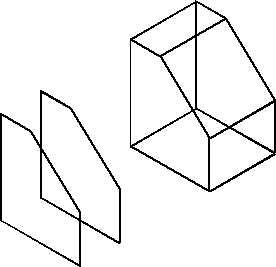
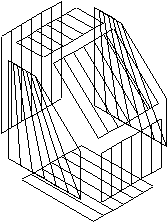
Рис. 6.2 – Формирование объемного объекта разверткой плоской области.
2. Поверхности вращения могут быть легко получены по команде, создающей поверхность вращением плоской грани вокруг определенной оси (эту процедуру можно трактовать как "круговую развертку"). При этом опять необходимо помнить, что создается не объемное тело, а генерируется только поверхность (Рис. 6.3).
3. Поверхности сопряжении и пересечений. Возможность построения плавного сопряжения одной поверхности с другой является наиболее мощным и часто используемым на практике средством поверхностного моделирования. Кроме этого, может быть доступно средство определения пересечения поверхностей.
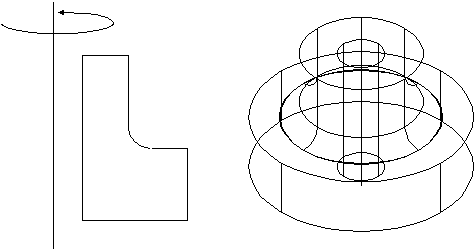
Рис. 6.3 – Получение поверхности вращения.
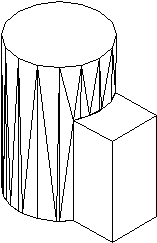
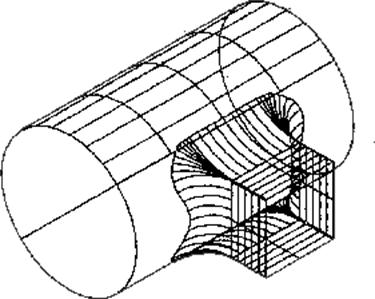
Рис. 6.4 – Поверхности сопряжения.
На Рис. 6.4 показано, как в трехмерном пространстве можно построить обычное и плавное сопряжения боковых поверхностей параллелепипеда и цилиндра. Проблема порождения результирующей поверхности в данном случае сводится к задаче построения методом сплайн-интерполяции особых кривых в трехмерном пространстве, "выходящих" из сторон квадрата и "входящих" в автоматически генерируемую кривую на поверхности цилиндра, по которой заданные поверхности должны пересекаться.
 2014-02-12
2014-02-12 1866
1866








