2014-02-12
4478
Система координат
Положение точки t в пространстве может быть описано в виде некоторых линейно независимых векторов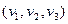 
А введя скаляры 
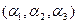можно описать вектор.
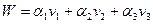
Структура взаимосвязей между системами координат
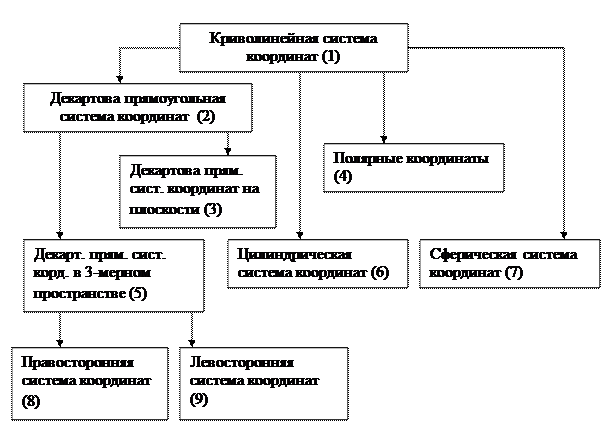
1) Базовая косоугольная система координат
Координаты определяются осями (х – ось абсцисс, у - ось ординат)
Расстояние определяется проекциями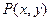 
4) Полярная система координат
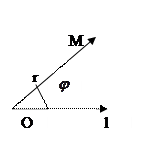
(.)0 – полюс,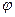
- полярный угол, r – полярное расстояние. M(r, )
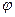Соответственно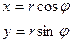 
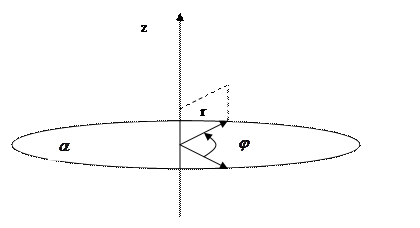Есть некая плоскость
Z проекция на точку M
7) Сферические системы координат
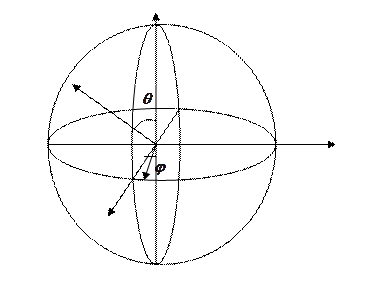
угол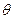 
- полярное расстояние
угол 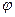- долгота
Соответственно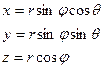 
1. 
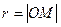
2.
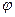
3.
Косоугольная система координат
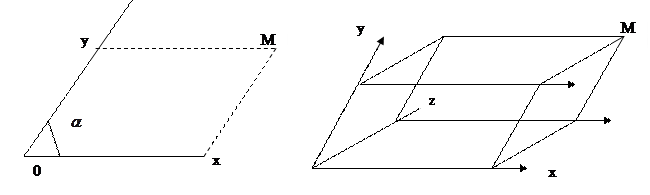
| Декартова система координат | M(x,y,z) | |
| Полярная | M( ) | |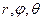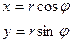
| Цилиндрическая | M( ) |  |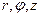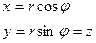
| Сферическая с коор. | M() |  |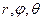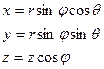
0 в середине экрана у Квартезианст.
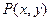(.) Все наши представления в векторах, в виде матрицы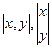 
Преобразование в компьютерной графике
- проекционное преобразование
- геометрические (аффинные) преобразования
& Геометрические преобразования в компьютерной графике.
Аффинные преобразования.
Преобразования связанные с некоторыми изменениями объекта.
- Перенос
- Поворот
- Масштабирование
! Св - во аффинных преобразований
Св-во1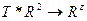 
всегда переводят прямую Q в T(a) так что множество точек прямой a отображается на множество (.) T(a)
Св-во 2 Если множество прямых а и b параллельны и задано некое аффинное преобразование T(a) и T(b) будут также параллельны
Дополнительные свойства
· Произведение 2-х аффинных преобразований также аффинное преобразование
· Для каждого преобразования Т существует такое Т – 1, которое тоже является аффинным преобразованием.
Рассмотрим последовательно аффинные преобразование.
(!) Масштабирование (scale)
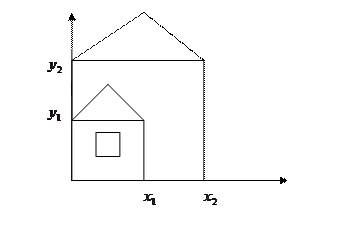
Если имеем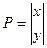 
, а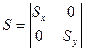 
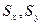- коэф. Мосштабиров.
, то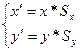 
Свойства преобразования масштабирования
- не сохраняется длинна
- не сохраняются углы
(!) Поворот (rotate)
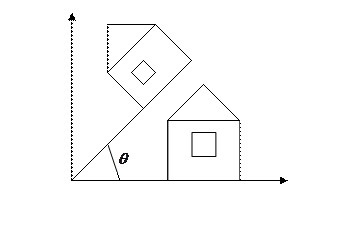
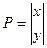
Если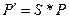 
то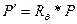 
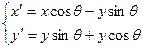
Соответственно матрица поворота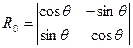 
(!) Перенос (Translate)
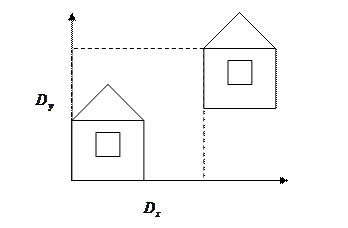
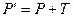
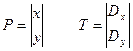
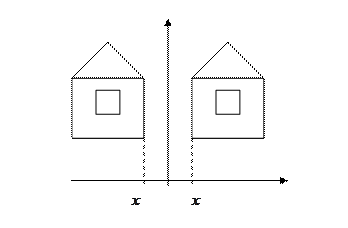
(!) Отражение (Reflection)
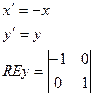
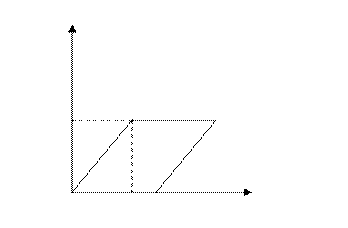
(!) Скос (самостоятельно)
