1. При транспонировании квадратной матрицы ее определитель не меняется: 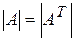 .
.
Вывод. Свойства определителей, сформулированных для строк, справедливы и для столбцов.
2. При перестановке двух строк (столбцов) определитель меняет знак на противоположный. Например, 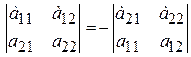 .
.
3. Определитель равен нулю, если:
а) он имеет нулевую строку (столбец) 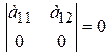 ;
;
б) он имеет пропорциональные (одинаковые) строки (столбец) 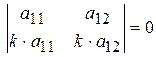 .
.
4. Общий множитель в строке (столбце) можно выносить за знак определителя. Например, 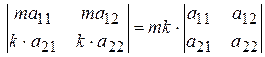 .
.
5. Определитель не изменяется, если к элементам какой-либо строки прибавить (вычесть) соответствующие элементы другой строки, умноженные на любое число.
Например, 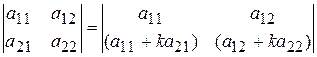 .
.
6. Если в определителе каждый элемент строки есть сумма двух слагаемых, то этот определитель равен сумме двух определителей:
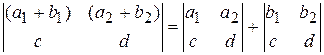 .
.
7. Определитель произведения двух квадратных матриц одного и того же порядка равен произведению определителей этих матриц:
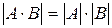 .
.
8. Определитель квадратной матрицы треугольного вида равен произведению элементов, стоящих на главной диагонали:

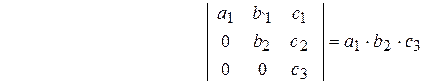 .
.
 2014-02-12
2014-02-12 1116
1116








