Закономерности распространения плоских упругих волн

Первой моделью, которую мы рассмотрим, станет модель идеального сжимаемого газа. Эта модель используется для описа­ния, например, распространение плоских, имеющая непосредственное отношение к процессам формирования и распространения воздушных удар­ных волн при ведении взрывных работ, а также к процессам детонации ПВВ, действию ударных волн в горных породах и т.д.

Идеальный совершенный газ характеризуется отсутствием в нем касательных напряжений, т.е. σ_ij = 0, (i ≠ j).При этом на­пряжение в точке определяется только шаровым тензором, не зависящим от ориентации площадки, на которой рассматривает­ся вектор напряжения 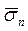. Так что напряжение в этом случае яв­ляется скалярной величиной, которую обычно принято обозна­чать буквой р. Кроме того, в аэрогидродинамике принято сжи­мающее напряжение считать положительным, а растягивавшее — отрицательным, так что в рассматриваемом случае уравнение неразрывности (19.2) и соотношение (19.4) об изменении ко­личества движения дают четыре скалярных уравнения

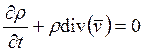; (19.6)

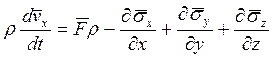
или

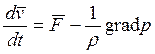
для пяти неизвестных p, ρ,v_x, v_y, v_z (второе векторное уравнение соответствует трем скалярным — по каждой оси координат). Уравнение же моментов количества движения превращается в тождество и новых соотношений для указанных величин не дает.

Распространение ударных и упругих волн в газах — быстропротекающие процессы, теплообмен их с окружавшей сре­дой не успевает существенно изменить их термодинамическое состояние. Поэтому приближенно такие процессы рассматрива­ются как процессы без теплообмена, а распространение упругих ноли — как процесс без изменения энтропии частиц. С учетом этого обстоятельства и невозможности существования вечного теплового двигателя второго рода для совершенных газов уста­новлено еще одно соотношение

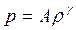(19.7)

где А — некоторая постоянная; 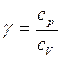; с_р —теплоемкость газа при постоянном давлении (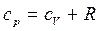); c_V — теплоемкость газа при постоянном объеме.

При этом постоянная А через начальные значения р ₀и ρ ₀ выражается соотношением 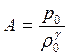, так что выражение (19.7) записывается в виде

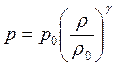(19.8)

и носит название адиабаты Пуассона.

Величина γ для многих газов при атмосферных условиях изменяется в сравнительно небольших пределах от 1,3 до 1,5. Для воздуха γ = 1,41, для ПД γ = 1,35.

Система уравнений (19.6) и (19.8) позволяет полностью рассчитать любой процесс, при этом по формуле Клапейрона

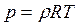(19.9)

может быть рассчитана и температура Т газа, где R = c_p-c_v — газовая постоянная, равная для воздуха 287,042 м²/с²·градус.

Скорость распространения упругих волн в газах определяет­ся соотношением

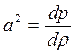(19.10)

что по адиабате Пуассона (19.8) дает выражение

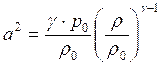(19.11)

Рассмотрим теперь распространение в воздухе плоской уп­ругой волны малой амплитуды. Направим ось X вдоль направ­ления движения волны. В этом случае все параметры волны бу­дут функциями только двух переменных — координаты X и времени t. Вследствие этого для упрощения записи индекс x у всех величин опустим, имея в виду, что v_x = v и т.д. Исходными для анализа этих волн являются уравнения (19.6) и (19.7). В рассматриваемом случае имеем

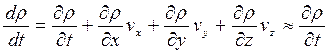
потому что 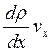есть произведение двух малых величин 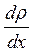и 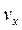и на порядок меньше 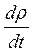; а величины 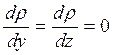, потому что ρ не зависит от Y и Z.

Таким образом, уравнение неразрывности преобразуется к следующему виду

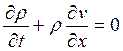(19.12)

Аналогичным образом преобразуется уравнение движения:

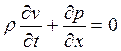(19.13)

Уравнения (19.12), (19.13) совместно с уравнением (19.8) составляют замкнутую систему уравнений для определения не­известных ρ,v,p. Причем, если принять одну из них за незави­симую переменную (например, ρ), то две других (соответствен­но, v u p), будут однозначно выражаться через первую.

Выполним некоторые преобразования и установим вид урав­нения, которому подчиняются ρ,v,p, описывающие распростра­нение упругих плоских волн малой амплитуды, приняв ρ за ос­новную независимую величину для трех из них. По правилу дифференцирования сложной функции с учетом (19.8) можно записать

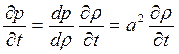(19.14)

Из уравнения (19.12) следует, что

.

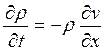Подставив полученную производную в уравнение (19.14), получим

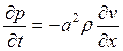. (19.15)

Уравнение (19.13) перепишем в виде:

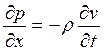(19.16)

Теперь продифференцируем первое уравнение в (19.15) по х,

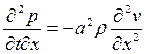, (19.17)

а уравнение (19.16) по t

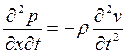. (19.18)

В уравнениях (19.17) и (19.18) равны левые части, следовательно, и правые части этих уравнений также равны

.

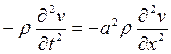Таким образом, получаем уравнение

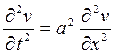, (19.19)

которое является однородным гиперболическим уравне­нием в частных производных второго порядка с постоянными ко­эффициентами и описывает распространение волн малой амплитуды, поэтому его называют волновым. Уравнение (19.19) имеет общее решение:

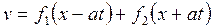(19.20)

где первый член описывает распространение волны в положитель­ном направлении оси X, авторой член — в отрицательном направ­лении оси X. Проведя аналогичные преобразования, получим, что и давление р будет удовлетворять аналогичному волновому уравне­нию, а его решение будет описываться формулой

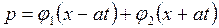(19.21)

Установим связь между функциями v и р. Рассмотрим для определенности только f ₁и φ ₁ и обозначим .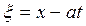

По второму уравнению (19.16) находим

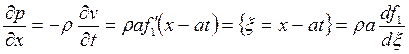(19.22)

Интегрируя уравнение (19.22) по х, получим

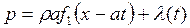(19.23)

Дифференцируем (1.5.23) по t

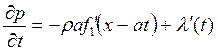(19.24)

Из уравнения (19.15) следует, что

.

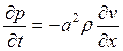Дифференцируем (19.21) по x

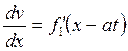(19.25)

Следовательно, поставляя (19.24) и (19.25) в (19.15) получим

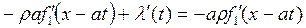
устанавливаем, что произ­вольная функция от времени λ '(t) = 0, а

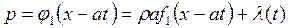(19.26)

с точностью до постоянной.

Постоянная, входящая в (19.26), определяется некоторыми начальными условиями. Учитывая, что f ₁ (x-at) = V соотноше­ние (19.26) можно переписать в виде

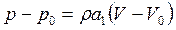(19.27)

где 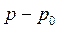— избыточное давление, возникающее при прохож­дении плоской волны, имеющей амплитуду V-V ₀ и начальные параметры движущегося газа р ₀и V ₀.

Из соотношений (19.20) и (19.21) следуют два очень важ­ных вывода:

• плоские упругие волны малой амплитуды распространяются по сплошной среде с постоянной скоростью;

• форма плоских упругих волн малой амплитуды по мере их
распространения в сплошной среде не изменяется.