Построить полигон, гистограмму и кумулянту по вариационному и интервальному ряду из примера 1.
Решение.
Полигон для вариационного ряда
 | |||||
 |
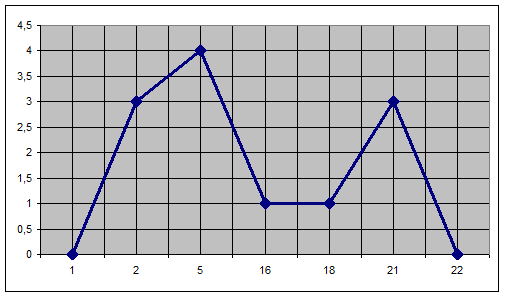
Полигон для интервального ряда
 | [2; 6) | [6; 10) | [10; 14) | [14; 18) | [18; 22) |
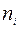 |
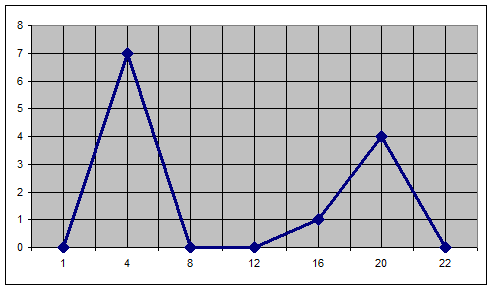
Гистограмма для интервального ряда:
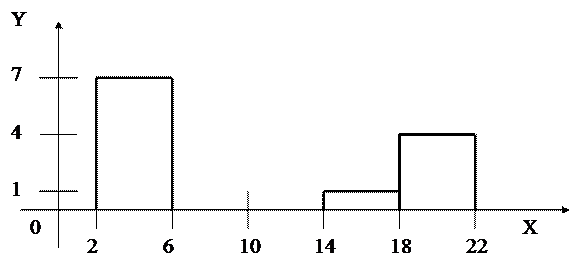
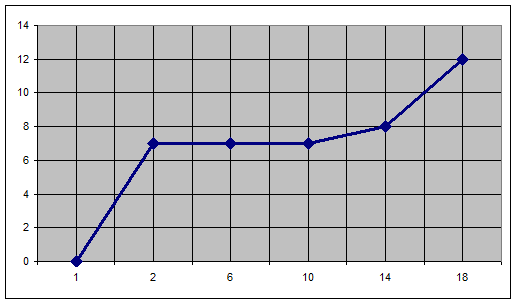
Кумулянта для вариационного ряда:
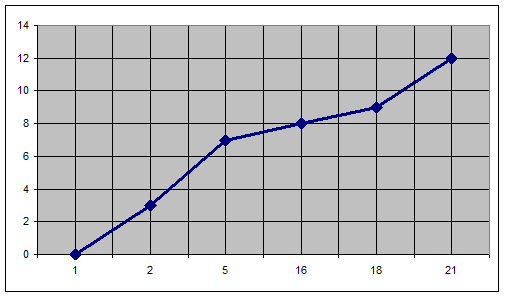
Кумулянта для интервального ряда:
§ 2. Выборочные характеристики
В этом параграфе мы рассмотрим ряд числовых параметров, которые характеризуют выборку.
Размахом вариации R называется разность между наибольшим и наименьшим значениями вариант: 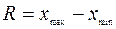 .
.
Медианой МВ называется значение признака, приходящегося на середину ранжированного ряда наблюдений.
Пусть проведено нечетное число наблюдений, т.е. n = 2 q – 1, результаты проранжированы и выписаны в следующем порядке: x(1), x(2),…, x(q–1), x(q), x(q+1),…, x(k). На середину ряда приходится значение x(q). Следовательно, МВ = x(q).
Пусть проведено четное число наблюдений, т.е. n = 2 q, тогда на середину ранжированного ряда приходится два значения x(q) и x(q+1). В этом случае за медиану принимают их среднее арифметическое, т.е. 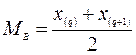 .
.
Модой МО называется такое значение признака, которое наблюдалось наибольшее число раз. Нахождение моды для дискретного вариационного ряда не требует каких-либо вычислений, так как ею является значение, которому соответствует наибольшая частота.
Выборочной средней называется величина
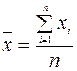
где n – объем выборки. Эту величину называют средней арифметической.
Если учесть частоты ni появления признака xi, то получим формулу
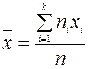 .
.
Эту величину называют средней взвешенной.
Геометрически выборочная средняя – это центр распределения.
Выборочной дисперсией (вариацией) называется величина
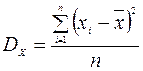 ,
,
где n – объем выборки.
Если учесть частоты ni появления признака xi, то получим формулу
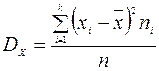 ,
,
где n – объем выборки.
Геометрически дисперсия является мерой рассеивания относительно средней (центра), но так как размерность дисперсии не совпадает с размерностью выборочной средней, используется корень из дисперсии, который называется стандартным отклонением или средним квадратическим отклонением 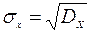 .
.
 2014-02-12
2014-02-12 1352
1352








