Характеристики генеральной совокупности обычно неизвестны. Задача заключается в их оценке по характеристикам выборочной совокупности.
Характеристики генеральной совокупности принято называть параметрами,а выборочной совокупности — оценками.
Пусть искомый параметр генеральной совокупности есть q0, а на основе выборки объема n определяется оценка q.
Для того чтобы выборочная оценка давала хорошее приближение оцениваемого параметра, она должна удовлетворять определенным требованиям (несмещенности, эффективности и состоятельности).
Несмещенность оценок. Оценка 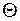 называется несмещенной,если ее математическое ожидание равно оцениваемому параметру
называется несмещенной,если ее математическое ожидание равно оцениваемому параметру 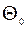 при любом объеме выборки, т.е.
при любом объеме выборки, т.е. 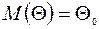 .
.
Если это не так, то оценка называется смещенной,а разность 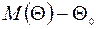 называется смещением.
называется смещением.
Выборочная средняя 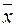 является несмещенной оценкойгенеральной средней m, так как
является несмещенной оценкойгенеральной средней m, так как 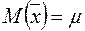 . Тем не менее оценка
. Тем не менее оценка 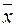 не единственная возможная несмещенная оценка m.
не единственная возможная несмещенная оценка m.
Выборочная дисперсия DX является смещенной оценкойгенеральной дисперсии 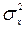 , при этом
, при этом
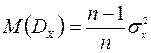
В качестве несмещенной оценки генеральной дисперсии используется величина (исправленная дисперсия)
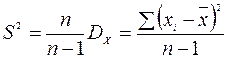
Величина S называется стандартным отклонением случайной величины в выборке.
Эффективность оценок. Несмещенная оценка q называется эффективной, если она имеет минимальную дисперсию по сравнению с другими выборочными оценками, т.е. 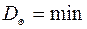 .
.
Предположим, что имеются две оценки параметра q0, рассчитанные на основе одной и той же информации (рис. 2). Оценка А является более эффективной, чем оценка В.
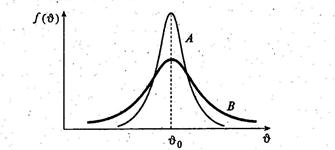
Выборочная средняя 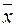 является эффективной оценкой генеральной средней, т.е. имеет наименьшую дисперсию в классе несмещенных оценок.
является эффективной оценкой генеральной средней, т.е. имеет наименьшую дисперсию в классе несмещенных оценок.
Состоятельность оценок. Оценка q называется состоятельной,если при n ® ¥ она стремится по вероятности к оцениваемому параметру q0, т.е.
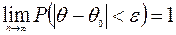 .
.
Иначе говоря, состоятельной называется такая оценка, которая дает точное значение для большой выборки независимо от входящих в нее конкретных наблюдений.
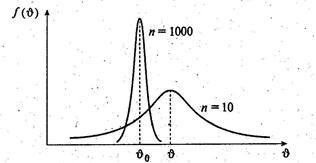
На рисунке показано, как при различном объеме выборки может выглядеть распределение вероятностей (состоятельная оценка, смещенная на малой выборке).
Теорема Чебышева закона больших чисел утверждает, что
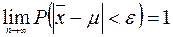 ,
,
то есть выборочная средняя 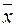 является состоятельной оценкой генеральной средней m.
является состоятельной оценкой генеральной средней m.
 2014-02-12
2014-02-12 727
727








