Тема 3. Смеси идеальных газов.
Занятие №6, 7
Газовая смесь - это смесь отдельных газов, не вступающих между собой в какие-либо химические реакции. Каждый газ (компонент) в смеси независимо от других газов полностью сохраняет все свои свойства и ведет себя так, как если бы он один занимал весь объем смеси.
Смесь идеальных газов, не вступающих в химические соединения, ведет себя как идеальный газ, а каждый входящий в смесь идеальный газ проявляет себя так, как если бы в ней не было других газов: распространяется по всему объему смеси и следует своему уравнению состояния.
В теплотехнических установках теплоноситель или рабочее тело часто представляют собой смесь газов при невысоком давлении, когда их можно рассматривать как идеальные газы. Схема получения такой смеси, состоящей из двух компонентов, показана на рис. 1.
Рис. 1
До смешения компоненты находятся в объемах V1 и V2 при одинаковом давлении p и одинаковой температуре T. Массы газов и их калорические свойства (внутренние энергии, энтальпии, теплоемкости и др.), естественно, различны. После того как убрана перегородка, газы вследствие диффузии перемешиваются, так что каждый из них занимает полный объем Vсм , а давление каждого газа будет равно парциальному давлению (давление отдельно взятого компонента газовой смеси. Общее давление газовой смеси является суммой парциальных давлений её компонентов. Парциальное давление одного идеального газа в смеси разных идеальных газов по определению равно давлению, которое будет оказываться, если он одиночку занимает тот же объём при той же температуре как и вся смесь. Идея теории состоит в том, что молекулы идеального газа настолько далеки одна от другой, что они не мешают друг другу) его в смеси p1 и p2, соответственно. При этом изменений температуры или давления не происходит.
Закон Дальтона: общее давление смеси идеальных газов равно сумме парциальных давлений каждого газа в смеси. Например, дана смесь идеального газа из азота (N2), водорода (H2) и гелия (He), тогда:
Pсмеси=Pазота+Pводорода+Pгелия или Р = Р1 + Р2 + Р3 +...Рn = ∑ Рi ,
где Pазота- парциальное давление азота,
Pводорода- парциальное давление водорода,
Pгелия- парциальное давление гелия.
Или где Р1, Р2, Р3...Рn – парциальные давления.
Закон аддитивности Амага ( Аддитивность (лат. additivus — прибавляемый) — свойство величин, состоящее в том, что значение величины, соответствующее целому объекту, равно сумме значений величин, соответствующих его частям, в некотором классе возможных разбиений объекта на части. Например, аддитивность объёма означает, что объём целого тела равен сумме объёмов составляющих его частей ): общий объем газовой смеси равен сумме парциальных объемов ее компонентов. Под парциальным объемом компонента смеси идеальных газов понимается объем, который занимал бы данный компонент при отсутствии остальных, находясь в такой же концентрации, под тем же давлением и при той же температуре:
V = V1 + V2 +...+ Vn
Состав такой смеси можно характеризовать следующими величинами:
-массовая доля i –того компонента:
gi =mi/mсм =mi/ ∑mi,
где mi и mсм –массы, соответственно, компонента и смеси;
-мольная доля i –того компонента:
xi =νi/νсм =νi/∑νi,
где νi и νсм –числа киломолей компонента и смеси;
- объемная доля i –того компонента:
ri =Vi/Vсм =Vi/ ∑Vi,
где Vi –объем компонента до смешения, Vсм –объем смеси.
Необходимо отметить, что для смеси идеальных газов объемная доля совпадает с мольной.
Между этими характеристиками состава смеси существуют очевидные соотношения:
gi =xi μi/ ∑xiμi,
xi =(gi/ μi)/ ∑(gi/μi),
где gi – массовая доля i-того компонента смеси,
xi – мольная доля i-того компонента смеси,
μi - масса киломоля.
Молекулярная масса смеси: μсм = μ1r1 + μ2r2+ … + μnrn,
где rn – объемная доля i-того компонента смеси.
Газовая постоянная смеси:
Rсм = g1R1 + g2R2 + … + gnRn = = Rμ (g1/μ1 + g2/μ2+ … + gn/μn) = 1 / (r1/R1 + r2/R2+ … + rn/Rn),
где gi – массовая доля i-того компонента смеси,
μi - масса киломоля.
Газовую постоянную смеси можно определить и через универсальную газовую постоянную:
Rсм = 8314 /μсм; Rсм = 8314∑(gi /μі),
где μсм – молекулярная масса смеси газов, кг/кмоль;
μі - молекулярная масса отдельного газа, кг/кмоль.
Теплоемкость тела – это величина, характеризующая способность тела изменять свою температуру с подводом или отводом теплоты. Она равна количеству теплоты, которое надо подвести к телу, чтобы изменить его температуру на 1 К:
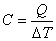 ,
,  Дж / К,
Дж / К,
Удельные массовые теплоемкости смеси - это теплоемкость, отнесенная к единице массы рабочего тела, Дж/(кг•К):
срсм. = g1ср1 + g2ср2 + … + gnсрn (изобарная теплоемкость),
сvсм. = g1сv1 + g2сv2 + … + gnсvn (изохорная теплоемкость),
где gi – массовая доля i-того компонента смеси.
Удельные молярные (молекулярные) теплоемкости смеси, Дж/(моль•К):
срμ см. = r1срμ 1 + r2срμ 2 + … + rnсрμ n ,
сvμсм. = r1сvμ 1 + r2сvμ 2 + … + rnсvμ n,
где ri – объемная доля i-того компонента.
Плотность газовой смеси, кг/м3: ρ = mсм / Vсм
Задача для ПР №2:
61. При температуре 27 °С и давлении 105 Па объем воздушного шара, заполненного гелием, равен 500 м3. Каким будет объем этого шара, если при подъеме в верхние слои атмосферы температура понизится до -33 °С, а давление станет равным 5·104 Па? Массу гелия считать постоянной.
Решение
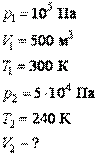
Из уравнения состояния идеального газа
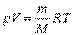 следует, что при условии
следует, что при условии 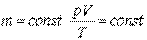 .
.
Поэтому выполняется равенство
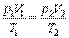 .
.
Из него получаем:
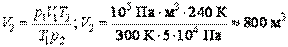 .
.
 2014-02-12
2014-02-12 7896
7896
