Лекция 9. Некоторые числовые характеристики одномерных случайных величин: начальные и центральные моменты, мода

Некоторые числовые характеристики одномерных случайных величин: начальные и центральные моменты, мода, медиана, квантиль, коэффициенты асимметрии и эксцесса. Числовые характеристики двумерных случайных величин: начальные и центральные моменты. Корреляционный момент и коэффициент корреляции. Коррелированность и зависимость случайных величин.

Определение 9.1. Начальным моментом порядка k случайной величины Х называется матема-тическое ожидание величины X^k:

ν _k = M (X^k). (9.1)

В частности, ν₁ = М (Х), ν₂ = М (Х ²). Следовательно, дисперсия D (X) = ν₂ – ν₁².

Определение 9.2. Центральным моментом порядка k случайной величины Х называется мате-матическое ожидание величины (Х – М (Х)) ^k:

μ _k = M ((Х – М (Х)) ^k). (9.2)

В частности, μ₁ = M (Х – М (Х)) = 0, μ₂ = M ((Х – М (Х))²) = D (X).

Можно получить соотношения, связывающие начальные и центральные моменты:

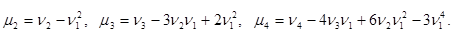
Мода и медиана.

Такая характеристика случайной величины, как математическое ожидание, называется иногда характеристикой положения, так как она дает представление о положении случайной величии-ны на числовой оси. Другими характеристиками положения являются мода и медиана.

Определение 9.3. Модой М дискретной случайной величины называется ее наиболее вероятное значение, модой М непрерывной случайной величины – значение, в котором плотность вероятности максимальна.

Пример 1.

Если ряд распределения дискретной случайной величины Х имеет вид:

то М = 2.

Пример 2.

Для непрерывной случайной величины, заданной плотностью распределения 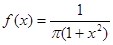, модой является абсцисса точки максимума: М = 0.

Замечание 1. Если кривая распределения имеет больше одного максимума, распределение называется полимодальным, если эта кривая не имеет максимума, но имеет минимум – анти-модальным.

Замечание 2. В общем случае мода и математическое ожидание не совпадают. Но, если распре-деление является симметричным и модальным (то есть кривая распределения симметрична от-носительно прямой х = М) и имеет математическое ожидание, оно совпадает с модой.

Определение 9.4. Медианой Ме непрерывной случайной величины называют такое ее значение, для которого

p (X < Me) = p (X > Me). (9.3)

Графически прямая х = Ме делит площадь фигуры, ограниченной кривой распределения, на две равные части.

Замечание. Для симметричного модального распределения медиана совпадает с математичес-ким ожиданием и модой.

Определение 9.5. Для случайной величины Х с функцией распределения F (X) квантилью порядка р (0 < p < 1) называется число К_р такое, что F (K_p) ≤ p, F (K_p + 0) ≥ p. В частности, если F (X) строго монотонна, К_р: F (K_p) = p.

Асимметрия и эксцесс.

Если распределение не является симметричным, можно оценить асимметрию кривой распреде-ления с помощью центрального момента 3-го порядка. Действительно, для симметричного распределения все нечетные центральные моменты равны 0 (как интегралы от нечетных функ-ций в симметричных пределах), поэтому выбран нечетный момент наименьшего порядка, не тождественно равный 0. Чтобы получить безразмерную характеристику, его делят на σ³ (так как μ₃ имеет размерность куба случайной величины).

Определение 9.6. Коэффициентом асимметрии случайной величины называется

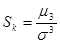
. (9.4)

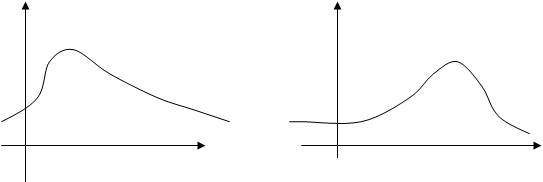
Рис.1. Рис.2.

В частности, для кривой, изображенной на рис.1, S_k > 0, а на рис.2 - S_k < 0.

Для оценки поведения кривой распределения вблизи точки максимума (для определения того, насколько «крутой» будет его вершина) применяется центральный момент 4-го порядка.

Определение 9.7. Эксцессом случайной величины называется величина

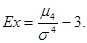(9.5)

Замечание. Можно показать, что для нормального распределения 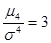, и, соответственно, Ех = 0. Для кривых с более острой вершиной Ех > 0, в случае более плоской вершины Ех < 0.