Статистическое описание и вычисление характеристик

Числовые характеристики статистического распределения: выборочное среднее, оценки дисперсии, оценки моды и медианы, оценки начальных и центральных моментов. Статистическое описание и вычисление оценок параметров двумерного случайного вектора.

Лекция 16.

Одна из задач математической статистики: по имеющейся выборке оценить значения числовых характеристик исследуемой случайной величины.

Определение 16.1. Выборочным среднимназывается среднее арифметическое значений случайной величины, принимаемых в выборке:

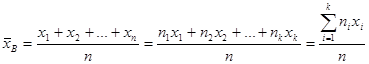, (16.1)

где x_i – варианты, n_i - частоты.

Замечание. Выборочное среднее служит для оценки математического ожидания исследуемой случайной величины. В дальнейшем будет рассмотрен вопрос, насколько точной является такая оценка.

Определение 16.2. Выборочной дисперсией называется

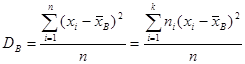, (16.2)

а выборочным средним квадратическим отклонением–

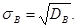(16.3)

Так же, как в теории случайных величин, можно доказать, что справедлива следующая формула для вычисления выборочной дисперсии:

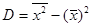. (16.4)

Пример 1. Найдем числовые характеристики выборки, заданной статистическим рядом

xi
ni

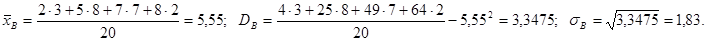Другими характеристиками вариационного ряда являются:

- мода М₀ – варианта, имеющая наибольшую частоту (в предыдущем примере М₀ = 5 ).

- медиана т_е - варианта, которая делит вариационный ряд на две части, равные по числу вариант. Если число вариант нечетно ( n = 2k + 1 ), то m_e = x_k+1, а при четном n =2k 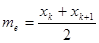. В частности, в примере 1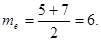

Оценки начальных и центральных моментов (так называемые эмпирические моменты) определяются аналогично соответствующим теоретическим моментам:

- начальным эмпирическим моментом порядка k называется

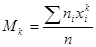. (16.5)

В частности, 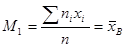, то есть начальный эмпирический момент первого порядка равен выборочному среднему.

- центральным эмпирическим моментом порядка k называется

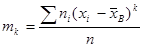. (16.6)

В частности, 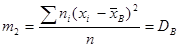, то есть центральный эмпирический момент второго порядка равен выборочной дисперсии.