2014-02-12
3973
Вернёмся к уравнению (7). Если в первом приближении полагать, что температура воздуха с высотой не меняется, т.е. считать, что Т =const (изотермическое приближение), то уравнение (7) легко интегрируется:
.
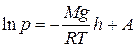Постоянная интегрирования А определяется из условия: при h= 0 давление р = р 0=1 атм. Это даёт: h =ln р 0. И тогда
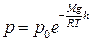. (9)
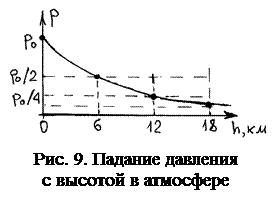
Эта формула называется барометрической и описывает изменение давления с высотой в изотермической модели атмосферы. Подстановка в (9) численных значений (М =0,029, g =9,8, R =8,31, Т =300) даёт, что давление атмосферы падает примерно в 2 раза на каждые 6 км высоты. График функции (9) показан на рис. 9.
Замечание. Если функцию Т (h) брать из адиабатной модели атмосферы, т.е. из (8), то уравнение (7) также легко интегрируется, но зависимость р (h) в этом случае будет более громоздкой.
Пример. Вычислить давление на вершине Эвереста в изотермическом приближении.
Решение. Полагая h =9000 м, М =0,029, Т =250 К (−23°С), из (9) получаем:
р = р 0 е −1,28≈0,28 р 0.
