Под гидравлической устойчивостью понимают способность системы теплоснабжения сохранять постоянный расход теплоносителя у абонентов при изменении условий работы других потребителей. Чем устойчивее система, тем меньше влияние гидравлического режима всей системы на гидравлический режим отдельных абонентов. При питании от общей тепловой сети разнородных тепловых потребителей невозможно без авторегулирования абонентов добиться высокой гидравлической устойчивости системы. Однако путем правильной регулировки можно значительно увеличить гидравлическую устойчивость.
Количественная оценка гидравлической устойчивости абонентов производится по коэффициенту гидравлической устойчивости: 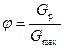 , (7.11)
, (7.11)
где G р – расчетный расход через абонент;
G max – максимальный возможный расход через абонент.
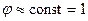 - для абонентов с авторегуляторами, т.к.
- для абонентов с авторегуляторами, т.к. 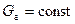 при всех гидравлических режимах.
при всех гидравлических режимах.
При отсутствии авторегуляторов φ значительно отличается от 1. Максимальная разрегулировка возникает при наибольшем отклонении действительного располагаемого напора в тепловой сети от расчетного значения у абонента (рис. 7.12):
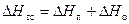 ;
; 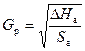 ;
;
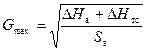 .
.
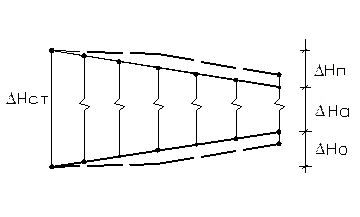
Рис. 7.12.
При отключении части абонентов от тепловой сети, расход в сети уменьшается и уменьшается располагаемый напор в тепловой сети, следовательно, увеличивается напор абонента. В пределе, когда 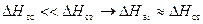 , что способствует максимальной степени изменения расхода у абонента
, что способствует максимальной степени изменения расхода у абонента 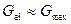 :
:
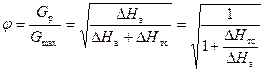 . (7.12)
. (7.12)
φ = 1 – для автоматизированных систем, абсолютно устойчивая система.; для неавтоматизированных систем φ = 1, если 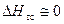 (т.е. при очень больших диаметрах трубопроводов).
(т.е. при очень больших диаметрах трубопроводов).
Таким образом, гидравлическая устойчивость системы тем выше, чем меньше потери в магистралях и чем больше потери у абонентов. При любых гидравлических режимах 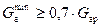 . Исходя из этого, можно определить потери в магистралях:
. Исходя из этого, можно определить потери в магистралях:
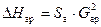 ;
; 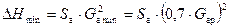 ;
;
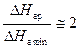 или
или 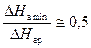 .
.
Система считается устойчивой, если потери давления в магистралях составляют 50 % от 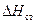 .
.
7.6. Расчет потокораспределения в концевых тепловых
сетях и тепловых сетях, питаемых от нескольких
источников
Тепловые сети городов представляют собой многокольцевые системы. Расчет таких систем – сложная задача, как правило, выполняется на ЭВМ. Т.к. водяные системы аналогичны электрическим, то принцип расчета потокораспределения в многокольцевых тепловых сетях основан на уравнениях Кирхгофа.
В зависимости от наличия у абонентов авторегуляторов, на практике решают две задачи: 1. Если у абонентов установлены регуляторы расхода РР, то известны расходы воды у абонентов (они постоянны) G i и сопротивления участков магистралей сети S i. Требуется определить G i по магистралям (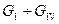 ); 2. Если у абонентов не установлены РР, то известен напор Н о в узле подвода сетевой воды к кольцу и сопротивления всех участков S i. Требуется определить расход воды в системе и по участкам сети.
); 2. Если у абонентов не установлены РР, то известен напор Н о в узле подвода сетевой воды к кольцу и сопротивления всех участков S i. Требуется определить расход воды в системе и по участкам сети.
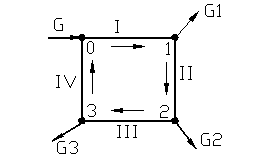
Рис. 7.13. Схема потокораспределения
1. Расчет потокораспреления в кольцевой сети с РР у абонентов (рис. 7.13). Вода со станции поступает в узел 0 и распределяется по участкам I и IV магистрали между абонентами 1-3. Расходы воды у абонентов G 1, G 2, G 3 заданы и поддерживаются постоянными регуляторами расхода на вводах. Суммарный расход воды: 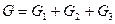 . Требуется определить G I, G II, G III и G IV. Условимся, что: а) приток воды в узел – “+”; отток воды из узла – “-“; б) ΔН потока, протекающего по часовой стрелке – “+”; ΔН потока, протекающего против часовой стрелки – “-“.
. Требуется определить G I, G II, G III и G IV. Условимся, что: а) приток воды в узел – “+”; отток воды из узла – “-“; б) ΔН потока, протекающего по часовой стрелке – “+”; ΔН потока, протекающего против часовой стрелки – “-“.
Первый закон Кирхгофа: алгебраическая сумма расходов воды в любом узле равна нулю.
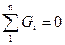 . (7.13)
. (7.13)
Второй закон Кирхгофа: алгебраическая сумма потерь напора для любого замкнутого кольца равна нулю.
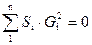 . (7.14)
. (7.14)
Расчет производится методом последовательного приближения:
1. Задать произвольно распределение расходов воды по участкам, удовлетворяющим первому закону Кирхгофа 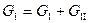 ;
; 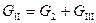 ;
; 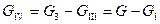 .
.
2. По второму закону определяем невязку потерь напора в кольце:
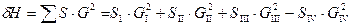 .
.
Если 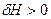 (положительно), то участки, в которых расход направлен по часовой стрелке – перегружены, а против часовой стрелки – недогружены.
(положительно), то участки, в которых расход направлен по часовой стрелке – перегружены, а против часовой стрелки – недогружены.
3. Для увязки потерь напора 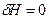 вводят увязочный расход
вводят увязочный расход 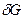 .
. 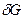 должен вычитаться из предварительно выбранного расхода на перегруженных участках и добавляться на недогруженных.
должен вычитаться из предварительно выбранного расхода на перегруженных участках и добавляться на недогруженных. 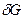 может быть определен из второго закона, если принять
может быть определен из второго закона, если принять 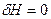 и ввести
и ввести 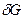 в правую часть уравнения:
в правую часть уравнения:
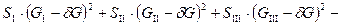
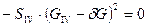 . (7.15)
. (7.15)
Решая это уравнение, и, пренебрегая членами, соединяющими 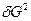 , получим:
, получим:
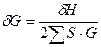 , где
, где 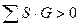 , (7.16)
, (7.16)
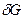 имеет тот же знак, что и
имеет тот же знак, что и 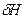 .
.
4. Уточняют расходы на участках и вновь проводят проверочный расход по второму закону.
Обычно удовлетворительные результаты получают после второй поравки.
2. Расчет потокораспределения в кольцевой сети без РР (рис. 7.13) сводится к определению точки водораздела в кольце, удовлетворяющей второму закону Кирхгофа. Первое уравнение Кирхгофа не может быть использовано, т.к. расходы воды у абонентов заранее не известны. Задача решается тоже методом последнего приближения:
1. Задать точку водораздела – точка 3.
2. Задать долю расхода φ, поступающего в точку 3 из III от G 3. Доля расхода, поступающего из IV, будет соответственно равна 1 – φ.
3. Сопротивление систем: 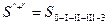 ;
;
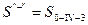 определяется по правилам сложения сопротивлений для последовательных участков и проводимостей, а для параллельных участков – как для радиальных сетей с ответвлениями. Т.к. в ответвление 3 поступает два потока воды из двух магистралей III и IV, то в соответствии с правилом, что при одновременном поступлении в систему нескольких потоков воды, каждый из потоков испытывает сопротивление, равное сопротивлению системы, деленному на квадрат долевого расхода данного потока, получим:
определяется по правилам сложения сопротивлений для последовательных участков и проводимостей, а для параллельных участков – как для радиальных сетей с ответвлениями. Т.к. в ответвление 3 поступает два потока воды из двух магистралей III и IV, то в соответствии с правилом, что при одновременном поступлении в систему нескольких потоков воды, каждый из потоков испытывает сопротивление, равное сопротивлению системы, деленному на квадрат долевого расхода данного потока, получим:
- поток из III → 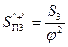 ;
;
- поток из IV → 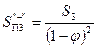 , где S 3 – сопротивление ответвления 3.
, где S 3 – сопротивление ответвления 3.
4. Расход воды в кольцевой сети:
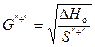 ;
; 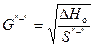 , где ΔН о – перепад в точке 0.
, где ΔН о – перепад в точке 0.
5. Определяют расход воды на всех участках сети по формуле:
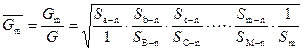 .
.
6. Проверяют выполнение условия. Если невязка будет положительной, то уменьшают долю расхода из III магистрали φ или если 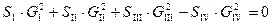 , то смещают точку водораздела в точку 2. При отрицательной невязке, соответственно, все наоборот.
, то смещают точку водораздела в точку 2. При отрицательной невязке, соответственно, все наоборот.
7. Уточняют расчет до тех пор, пока не будет выполняться второй закон Кирхгофа.
3. Расчет потокораспределения в сети, питаемой от нескольких источников (рис. 7.14).
В современных системах теплоснабжения обычно используют закольцованные сети от нескольких источников. Применение таких схем дает возможность повысить технико-экономические показатели по сравнению с обычными радиальными системами: возможность перераспределения нагрузки между источниками; при ремонтах возможно отключение одного или нескольких источников; сокращается резерв оборудования; возможно применение количественно-качественного регулирования, которое дает экономию на перекачку теплоносителя до 25 % от годового.
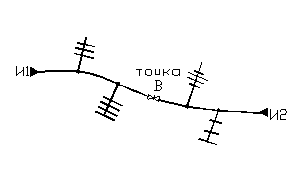
Рис. 7.14.
В магистралях таких сетей появляются точки водораздела, представляющие собой точки встречи потоков воды от разных источников. Положение этих точек определяется распределением расходов, а, следовательно, и распределением нагрузок между источниками.
Положение точки В зависит от сопротивления сети, распределения нагрузки вдоль магистралей, напора сетевых насосов и т.д.
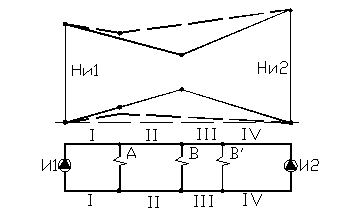
Рис. 7.15.
Точка водораздела в таких тепловых сетях определяется следующим образом (рис. 7.15). Задаются произвольными расходами воды на участках магистралей, исходя из первого закона Кирхгофа. Определяют невязки напора по второму закону Кирхгофа. Если при предварительно выбранном распределении воды в сети водораздел выбран в точке В, то для этого условия второй закон Кирхгофа:
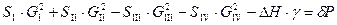 , (7.16)
, (7.16)
где 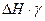 – разность напоров на коллекторах станций, Па;
– разность напоров на коллекторах станций, Па;
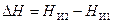 .
.
Определяют увязочный расход: 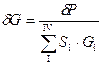 . (7.17)
. (7.17)
Уточняют расходы по магистралям.
Для обеспечения надежности работы тепловые сети иногда проектируют кольцевыми от первого источника (рис. 7.16). Такая сеть может рассматриваться как частный случай тепловой сети, питаемой от двух источников (рис. 7.17), с одинаковыми располагаемыми напорами на коллекторах станций.
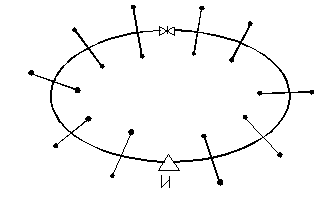
Рис. 7.16. Кольцевая схема тепловой сети от первого источника
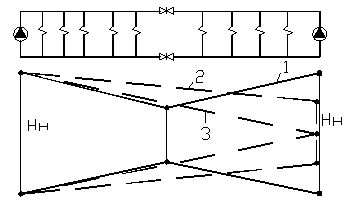
Рис. 7.17. Кольцевая схема тепловой сети от двух источников:
1 – нормальный режим; 2 – режим для нормальной работы
при аварии; 3 – фактический режим при аварии
Расчет в такой тепловой сети выполняют точно также, как для двух источников с учетом:
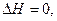 т.к.
т.к. 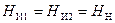 .
.
8. КОМПЕНСАЦИЯ ТЕМПЕРАТУРНЫХ УДЛИНЕ-
НИЙ ТРУБОПРОВОДОВ ТЕПЛОВОЙ СЕТИ И
8.1. Самокомпенсация
Прежде, чем предусматривать специальные устройства для компенсации температурных удлинений трубопроводов, необходимо использовать самокомпенсацию тепловых сетей (углы поворота 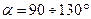 , Г – образные и Z – образные участки).
, Г – образные и Z – образные участки).
1. Расчет Г – образных узлов для канальной прокладки ( рис. 8.1 ).
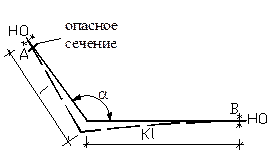
Рис. 8.1. Схема Г-образного компенсатора (канальная прокладка)
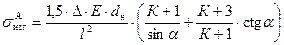 , (8.1)
, (8.1)
где 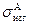 - напряжение изгиба, кГ/cм 2;
- напряжение изгиба, кГ/cм 2;
Δ – удлинение короткого плеча, см: 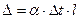 ;
;
α = 0,012 – коэффициент линейного удлинения для углеродных сталей, 1/ К;
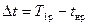 , ºС; (8.2)
, ºС; (8.2)
Е = 2ּ106 – модуль упругости, кГ/см ²;
d н – наружный диаметр трубы, см;
l – длина короткого плеча, см;
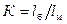 - отношение большего плеча к меньшему;
- отношение большего плеча к меньшему;
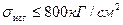 ; если σ не прошло, то надо сдвинуть одну из опор, т.е. выбрать
; если σ не прошло, то надо сдвинуть одну из опор, т.е. выбрать 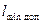 .
.
Для бесканальной прокладки ( рис. 8.2 ) расчет ведут по тем же формулам.
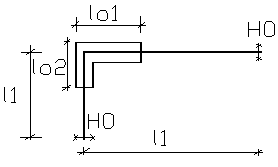
Рис. 8.2. Схема Г-образного компенсатора (бесканальная прокладка)
2. Расчет Z – образных участков (рис. 8.3).
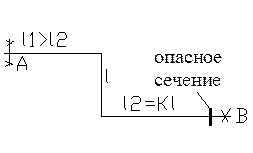
Рис. 8.3. Схема Z-образного компенсатора
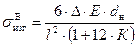 , (8.3)
, (8.3)
где l – длина перемычки, см;
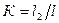 - отношение короткого плеча к перемычке.
- отношение короткого плеча к перемычке.
Если σ не проходит, то отодвигаем или опору, или перемычку.
8.2. Компенсаторы
Для компенсации на прямых участках трубопроводов расчитывают специальные компенсаторы: П–образные – для любых давления и температуры теплоносителя, любой прокладки и диаметров; сальниковые при Р ≤ 2,5 МПа, Т ≤ 300 ºС и d у ≥ 100 мм; сильфонные при Р ≤ 2,5 МПа, Т ≤ 200 ºС, t н ≤ -40 ºС и d у ≥ 100 мм. При гидравлическом расчете трубопроводов компенсаторы учитываются как местные сопротивления. Количество компенсаторов на участке трубопровода определяется по l доп. l доп определено для каждого d у из условия, чтобы трубопровод был жестким стержнем и не прогибался: l доп = f (d у, вид прокладки).
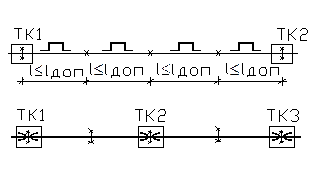
Рис. 8.4. Монтажные схемы участков тепловой сети
Если принимают сальниковые компенсаторы, то их устанавливают спарено, т.к. для их обслуживания на трассе делают специальные теплофикационные камеры (ТК).
Вылет П – образного компенсатора:  , см, (8.4)
, см, (8.4)
где b – ширина компенсатора, см;
Δ – удлинение трубопровода на участке между неподвижными опорами, см;
d – наружный диаметр трубопровода, см;
σ изг = 1100 кГ/см ² - для П – образных компенсаторов со сварными отводами. Решают методом последовательного приближения или задают l = b. Для лиро- и L образных компенсаторов 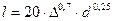 , см.
, см.
8.3. Расчетные нагрузки на трубопроводы
При расчете изгибающих напряжений и деформаций трубопровод, лежащий на свободных опорах, рассматривается как многопролетная балка (рис. 8.5). При одинаковой длине пролета между свободными опорами максимальный изгибающий момент в многопролетном трубопроводе возникает на опоре:
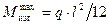 , (8.5)
, (8.5)
где l – длина пролета между опорами, м;
q – удельная нагрузка на единицу длины трубопровода, Н/м:
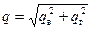 ; (8.6)
; (8.6)
q в – удельная вертикальная нагрузка от массы трубы, теплоносителя, теплоизоляции и снега, Н/м;
q г – удельная горизонтальная нагрузка от ветрового давления, Н/м:
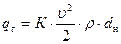 ; (8.7)
; (8.7)
К – аэродинамический коэффициент: 0,7 – для одиночной трубы; 1 – для двух и более труб;
υ – скорость ветра, м/с;
ρ – плотность воздуха, кг/м 3;
d н – наружный диаметр изолированного трубопровода, м.
Снеговая и ветровая нагрузка учитываются только для надземной прокладки тепловых сетей. Значение удельной снеговой нагрузки подсчитывается из нагрузки снега, приходящейся на 1 м² горизонтальной площади изолированного трубопровода, которая в среднем 500-1000 Н/м ².
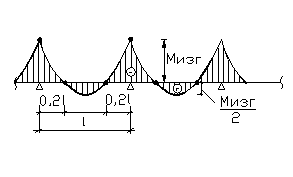
Рис. 8.5. Схема изгибающих напряжений и деформаций
трубопровода
Изгибающий момент, возникающий в середине пролета:
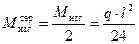 ; на 0,2ּ l от опоры М изг = 0. (8.8)
; на 0,2ּ l от опоры М изг = 0. (8.8)
Максимальный прогиб располагается посередине пролета.
Пролет между свободными опорами определяется из условия: 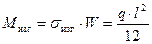 , (8.9)
, (8.9)
где σизг – допустимое изгибающее напряжение, ориентировочно σизг = 35 МПа;
W – момент сопротивления трубы (по справочнику как f (d)), м³.
Тогда длина пролета:
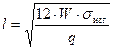 ; (8.10)
; (8.10)
l можно определить по приближенной формуле: 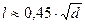 - точность ± 100 мм.
- точность ± 100 мм.
8.4. Усилия на неподвижные опоры
Усилия, воспринимаемые неподвижной опорой, складываются из неуравновешенных сил внутреннего давления, сил трения в подвижных опорах и сальниковых компенсаторах и сил упругой деформации П – образных компенсаторов и самокомпенсации:
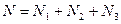 , Н (8.11)
, Н (8.11)
Осевое усилие от внутреннего давления теплоносителя:
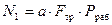 , Н, (8.12)
, Н, (8.12)
где а – коэффициент, учитывающий передачу усилия от внутреннего давления теплоносителя на опору: 0 – разгруженные неподвижные опоры (РНО); 1 – неразгруженные неподвижные опоры (ННО);
Р раб – внутреннее рабочее давление в трубопроводе; по СНиПу (п.7.6) – Р под у ТЭЦ, Па;
F тр - площадь поперечного сечения трубопровода по внутреннему размеру, м ².
Результирующая реакция подвижных опор:
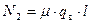 , Н, (8.13)
, Н, (8.13)
где µ - коэффициент трения на неподвижных опорах;
q в – вес 1 пм трубы в рабочем состоянии, Н/м;
l – длина трубопровода от неподвижной опоры до угла поворота или сальникового компенсатора, м.
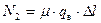 ;
; 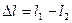 . (8.14)
. (8.14)
Силы трения в сальниковых компенсаторах:
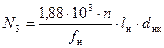 , Н, и (8.15)
, Н, и (8.15)
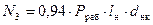 , Н, (8.16)
, Н, (8.16)
где n – число болтов компенсатора, шт;
f н – площадь поперечного сечения набивки компенсатора:
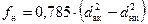 , м ²; (8.17)
, м ²; (8.17)
d вк – внутренний диаметр корпуса компенсатора, м;
d нк – наружный диаметр патрубка компенсатора, м;
l н – длина слоя набивки по оси компенсатора, м;
Р раб – рабочее давление теплоносителя, Па.
Из всей усилий, действующих на неподвижную опору, наиболее значительным является неуравновешенная сила внутреннего давления. По сравнению с этой силой, остальные реакции, действующие на неподвижную опору, невелики. В приближенных расчетах можно усилия на неподвижную опору определить как: 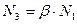 , где β – коэффициент, учитывающий N 3 как долю от N 1 (определяется по справочнику или учебнику): при d у = 100 мм β = 0,54; при d у = 500 мм β = 0,24; при d у = 100 мм β = 0,1. Для облегчения конструкции неподвижных опор надо стремиться к уравновешиванию осевых сил внутреннего давления.
, где β – коэффициент, учитывающий N 3 как долю от N 1 (определяется по справочнику или учебнику): при d у = 100 мм β = 0,54; при d у = 500 мм β = 0,24; при d у = 100 мм β = 0,1. Для облегчения конструкции неподвижных опор надо стремиться к уравновешиванию осевых сил внутреннего давления.
Неподвижные опоры делятся на разгруженные (РНО) и неразгруженные (ННО) (рис. 8.6). РНО – осевая реакция внутреннего давления не передается; ННО – воспринимают осевую реакцию внутреннего давления.
Для ННО: 
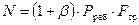 , Н. (8.18)
, Н. (8.18)
Для РНО: 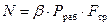 , Н. (8.19)
, Н. (8.19)
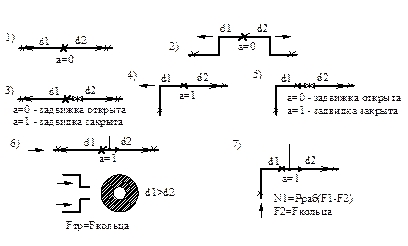
Рис. 8.6. Расчетные схемы неподвижных опор: 1, 2 – РНО; 3-7 – ННО
 2014-02-13
2014-02-13 2573
2573








