Метод подобия как основа исследования

Многообразие материального мира требует применения самых разнообразных способов его изучения. Одним из основных приемов разработки общих теоретических положений является обобщение.

Обобщение – есть средство перехода от познания частных явлений к познанию общих. Оно заключается в исследовании таких свойств и явлений материального мира, которые характеризуют не единичное явление, а целый класс однородных в данном отношении явлений. Обобщение имеет огромное значение в теории подобия для выделения из класса однородных явлений группы подобных между собой явлений. Изучив одно из подобных явлений, результаты исследования можно распространить на всю группу подобных явлений данного класса.

Теория подобия – есть учение о методах научного обобщения эксперимента. Она отвечает на вопрос, как нужно поставить опыт и обработать полученные данные, чтобы их можно было распространить на все подобные явления. Всякое явление природы представляет собой систему материальных тел, которая за счет протекания в ней различных процессов претерпевает определенное изменение состояния.

Подобными явлениями называют системы тел, геометрически подобные друг другу, в которых протекают процессы одинаковой физической природы и в которых одноименные величины, характеризующие явления, относятся между собой как постоянные числа. Принцип выделения группы подобных явлений из класса однородных можно уяснить на следующем простом примере.

Из класса однородных аппаратов (допустим, барабанных сушилок) выделяют группу подобных аппаратов, отличающихся только масштабом. Если аппарат и его модель геометрически подобны, то L₂ = cL₁ и D₂ = cD₁, где индекс “2” относится к промышленному аппарату, а индекс “1” – к модели. Для данной пары аппаратов величина масштабного множителя “ c ” является константой геометрического подобия (с = const). Подобие этой пары аппаратов можно выразить и другим способом – посредством инвариантов подобия. Для рассмотренного примера геометрического подобия можно записать

с = L₂/L₁ и с = D₂/D₁, или L₂/L₁ = D₂/D₁,

откуда

L₁/D₁ = L₂/D₂ = i_L = inv,

где i_L – инвариант геометрического подобия, представляющий собой безразмерное отношение двух размеров малого барабана (модели), равное отношению сходственных размеров подобного ему производственного барабана.

Инварианты подобия представляют собой выражение величин в относительных единицах. В приведенном примере один размер (длина) подобных аппаратов выражен в относительных единицах. В качестве масштаба принят их другой размер (диаметр).

Отличие константы подобия и инварианта заключается в том, что константа сохраняет постоянное значение во всех точках системы, но она изменяется, когда одна пара подобных явлений заменяется другой парой той же группы. Инвариант подобия, наоборот, различен для разных точек системы, но он не меняется при переходе от одного явления к любому другому подобному ему, т.е. сохраняет одно и то же значение в сходственных точках всех групп подобных явлений.

Отметим еще одно важное свойство констант подобия: входящие в них одноименные величины могут взаимно заменяться, т.е. отношение самих величин можно заменять отношениями приращений этих величин. Например:

.

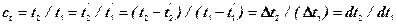При рассмотрении сложных процессов, которые определяются многими физическими величинами, выбирать произвольно константы подобия этих величин нельзя. Для таких процессов при выборе констант подобия имеются ограничения, которые находят, исследуя уравнения, описывающие процесс.

Рассмотрим правила выбора констант подобия на конкретном примере уравнения теплопроводности для плоской однослойной (однородной) стенки толщиной δ с теплопроводностью λ (рис. 2.1) при стационарном процессе. Пусть t₁>t₂. Требуется определить плотность теплового потока q, проходящую через стенку. Так как t₁ > t_2, то t_{с т 1} > t _{ст 2} . Пусть значения коэффициента теплоотдачи на горячей стороне α_{1 ,} на холодной – α₂.

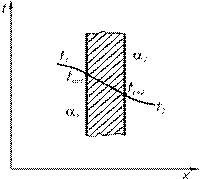
Рисунок 2.1 – Теплопередача через однородную плоскую стенку

На основании закона Фурье, плотность теплового потока, как известно, будет равна

,

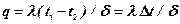где 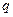– плотность теплового потока; 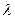– теплопроводность материала стенки; 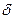– ее толщина; t₁ и t₂ – постоянные температуры на поверхностях стенки.

Пусть первая – основная – система характеризуется значениями параметров, 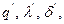а вторая – значениями 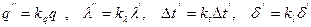. Значения параметров второй системы получены путём умножения значений параметров первой системы на соответствующие константы подобия. Тогда для первой системы 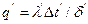, а для второй .

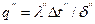Разделив почленно эти равенства одно на другое, получим:

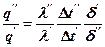или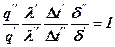

Подставляя вместо отношения величин их константы подобия, имеем

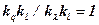. (2.1)

Функции типа уравнения (2.1), связывающие константы подобия, называются индикаторами подобия и обозначаются буквой j. Из уравнения (2.1) следует весьма важный вывод: при выборе числовых значений констант подобия для группы подобных явлений необходимо соблюдение условия j=1, т.е. выбор значений констант подобия не произволен.

Требования к выбору констант подобия, обусловленные уравнением (2.1) для рассматриваемого примера, можно представить и в другом, более удобном виде. Действительно, если в указанном уравнении константы подобия представить как отношения соответствующих параметров и все величины с одним штрихом сгруппировать в левой части уравнения, а с двумя штрихами – в правой, то получим

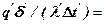
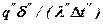или 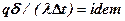. (2.2)

Уравнение (2.2) иллюстрирует основное свойство подобных явлений, заключающееся в том, что для всех подобных систем существуют безразмерные комплексы величин, которые сохраняют одно и то же значение.

Эти комплексы носят название инвариантов, что означает “неизменяемые”, или критериев подобия. Обозначение const в уравнении (2.2) не применяется, т. к. речь идёт об одинаковых величинах в различных системах и эти величины не обязательно должны быть постоянными.

При выводе формулы (2.2) был рассмотрен пример, в котором основное уравнение 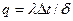задано в конечной форме. Если основное уравнение будет задано в дифференциальной форме, то все предыдущие результаты останутся прежними. При этом, как показывается в общей теории подобия, для нахождения критериев подобия необходимо в исходном уравнении отбросить все индексы, знаки сумм, символы, выражающие действие дифференцирования и т.п., ибо эти упрощения не изменяют констант подобия.

Поэтому основная ценность неинтегрируемых дифференциальных уравнений (например, процесса конвективного теплообмена Фурье-Кирхгофа, движения вязкой капельной жидкости Навье-Стокса и др.) состоит в том, что они позволяют установить критерии подобия для описываемых ими явлений.

В качестве примера найдём критерии подобия из дифференциального уравнения теплопроводности Фурье-Кирхгофа:

,

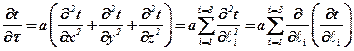где 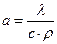– коэффициент температуропроводимости, l₁ = х, l₂ = y, l₃ = z.

Отбросив знаки суммирования и дифференцирования, в левой части уравнения получим приведенный комплекс 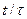, а в правой – 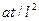, тогда

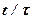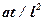= или 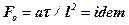. (2.3)

Полученный комплекс является искомым критерием подобия, который называется критерием Фурье (F₀), а при выборе констант подобия в этом случае должно выполняться условие .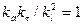

Коэффициент подобия 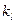представляет собой отношение отрезков, соединяющих в первой и второй системах две сходственные точки. Поэтому под размером в критериях подобия можно понимать любой геометрический размер; нужно только, чтобы для всех систем критерий вычислялся по этому размеру. Характерный размер, вводимый в критерий подобия, называется определяющим размером системы. Обычно для труб определяющим размером является диаметр, для плит – их толщина и т.д.

Заметим также, что все критерии подобия, в состав которых входит время 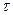, называются критериями гомохронности (греч. chronos – время), т. к. этими критериями определяется константа подобия (масштаб) времени через константы подобия других физических величин.