Свойства независимых событий

1. Если Р(В)>0, то для независимых событий А и В

Р(А/В)=Р(А) (1’)

Доказательство:

–

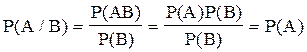Замечание: Иногда определение независимости событий дают на основе (1’). События А и В называются независимыми, если появление одного из них не влияет на вероятность появления другого.

2. Если А и В независимы, то независимы и 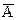и В; А 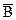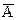и ; и .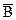

Доказательство: Докажем первое утверждение.

P(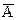 B)=P(B-AB)=P(B)-P(AB)=P(B)-P(B)P(A)=

=P(B)(1-P(A))=P(B)P().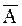

Доказательство второго утверждения аналогично. Докажем третье утверждение.

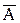
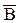P( )=P(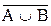)=1-P(AÈB)=1-P(A)-P(B)+P(AB);

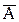P()P(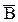)=(1-P(A))(1-P(B))=1-P(A)-P(B)+P(AB)

Сравнивая эти равенства, видим, что у них одинаковы правые части, следовательно

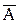
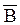Р(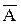 )=Р()Р() –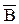

3. Пусть А и В₁ независимы, А и В₂ независимы, причем В₁В₂=Æ, тогда А и В₁+В₂ - независимы.

Доказательство:

P(A(В₁+В₂))=P(AВ₁+ AВ₂)= P(A)P(В₁)+P(A)P(В₂)=

=P(A)(P(В₁)+P(В₂))=P(A)P(В₁+В₂) –

4. Два несовместных события всегда зависимы, т.к. появление одного исключает появление другого

Если А и В несовместны (АВ=Æ), причем P(А)>0, P(B)>0, то Р(А/В)=Р(В/А)=0.

Доказательство: P(A/B)= …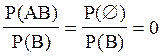

Независимость событий в совокупности: События А₁,А₂,..., А_n называются независимыми в совокупности, если любое из них не зависит от любой комбинации (произведения) любого числа других. Для независимых событий правило умножения принимает вид:

P(А₁А₂...А_n)=P(А₁)P(А₂)...P(А_n)

или короче, пользуясь знаком произведения:

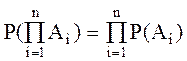
Т.е. вероятность произведения нескольких независимых событий равна произведению вероятностей этих событий.