При разработке системы возникает задача: обеспечить максимальную надежность (используя резервирование) не превысив заданного значения «веса» системы (стоимость, масса, объем и т.д.).
Пусть основная подсистема состоит из N последовательно соединенных элементов. Для каждого элемента используется постоянное нагруженное резервирование с Mi элементами, 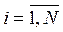 . Вероятность безотказной работы
. Вероятность безотказной работы
i -го элемента Pi(t), а его вес Wi.
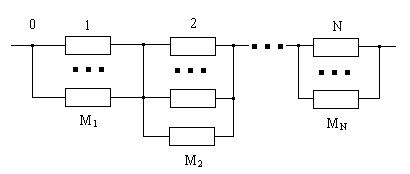
Рис.35. Система с постоянно включенным нагруженным резервом.
Вероятность безотказной работы системы с раздельным нагруженным резервом.
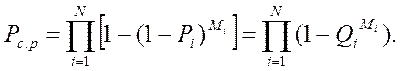 (127)
(127)
«Вес» системы с резервом
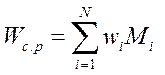 ,
, 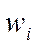 -вес элемента. (128)
-вес элемента. (128)
Задача сводиться к нахождению целых чисел Mi≥1,при которых
Рс.р= Рс.max,
а «вес» системы
Wc.p≤Wз,
где Wз – заданное значение ограничивающего фактора.
Существует и другая (обратная) задача: необходимо обеспечить заданную надежность резервированной системы (Рс.р=Рз) при минимуме «веса» (Wc.p=Wc.min).
Для решения сформулированных задач могут быть применены различные методы:
· метод неопределенных множителей Лагранжа,
· метод наискорейшего спуска,
· метод динамического программирования.
 2015-01-22
2015-01-22 393
393








