Расчеты на прочность

Балки рассчитывают на прочность по наибольшим нормальным напряжениям, возникающим в их поперечных сечениях. При поперечном изгибе балок наряду с нормальными возникают и касательные напряжения, обусловленные наличием поперечной силы, но они в подавляющем большинстве случаев невелики и при расчетах на прочность не учитываются.

Прочность балки обеспечена, если наибольшие по абсолютному значению нормальные напряжения, возникающие в опасном сечении, не превышают допустимых. Для балки, поперечные размеры которой по всей длине постоянны, опасное сечение то, в котором возникает наибольший по модулю изгибающий момент. Наибольшие нормальные напряжения возникают в точках опасного поперечного сечения, максимально удаленных от нейтральной оси. Эти точки принято называть опасными. Значения максимальных напряжений в опасных точках найдем по формуле:
,
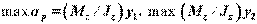где 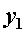и 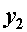- расстояния от нейтральной оси до наиболее удаленных точек соответственно в растянутой и сжатой зонах сечения.

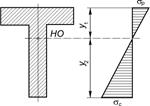Рисунок 1

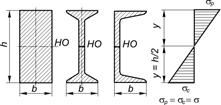
Если материал балки хрупкий, например закаленная сталь, чугун, текстолит и др., то расчет на прочность при изгибе проводят по напряжениям растяжения и сжатия. У хрупких материалов предел прочности при сжатии выше предела прочности при растяжении 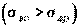. Следовательно, поперечным сечениям балок из хрупких материалов целесообразно придавать асимметричную форму относительно нейтральной оси (рис. 1) и располагать балку так, чтобы большая часть материала находилась в растянутой зоне.

Таким образом, при расчетах балок из хрупкого материала используются два условия прочности:
для растянутой зоны ;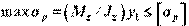
для сжатой зоны .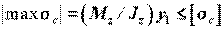

Причем наилучшее использование материала происходит при форме сечения, удовлетворяющей условию .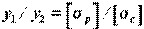

Рисунок 2

При расчете балок из пластичных материалов, например коуглеродистой стали или цветных металлов, допускаемые напряжения растяжения и сжатия одинаковы: 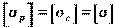. Поэтому для таких балок целесообразными являются сечения, симметричные относительно нейтральной оси (рис. 2), так как в этом случае наиболее удаленные точки в растянутой и сжатой зонах сечения располагаются на одинаковом расстоянии y = h/2 от нейтральной оси. И, следовательно, .

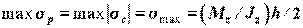Разделим числитель и знаменатель правой части этого равенства на h/2: .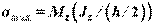

Величина 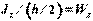, выражаемая в 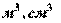или 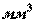, называется моментом сопротивления сечения при изгибе.
Для прямоугольного сечения (рис. 2), размеры которого 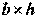, момент сопротивления .
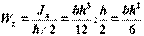Для круглого сечения .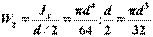

Наиболее экономичными при изгибе являются такие формы сечения, при которых материал бруса расположен как можно дальше от нейтральной оси. У таких брусьев при наименьшей затрате материалов получается наибольший момент сопротивления 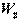. Поэтому и возникли профили стандартного проката (рис. 2), все необходимые геометрические характеристики которых содержатся в ГОСТ 8239-72 "Сталь горячекатаная. Балки двутавровые", ГОСТ 8240-72 "Швеллеры".

Таким образом, наибольшие напряжения растяжения или сжатия в симметричном относительно нейтральной оси сечения находят по формуле 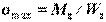и условие прочности балки из пластичного материала имеет вид 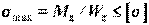, исходя из которого выполняют три вида расчетов.

Проектный расчет. Приняв 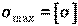, по изгибающему моменту 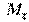в опасном сечении находят требуемое значение момента сопротивления: 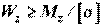. Затем, исходя из принятой для балки формы поперечного сечения, находят его размеры.

Расчет допускаемой нагрузки выполняется при 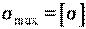по формуле 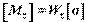. Затем, исходя из схемы нагружения балки, находят допускаемое значение нагрузки.

Проверочный расчет. Определив максимальный изгибающий момент и момент сопротивления сечения, находят по формуле значение 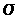и сравнивают его с .

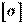Аналогично выполняют расчеты балок из условия прочности для растянутой зоны и условия прочности для сжатой зоны.