Химическая термодинамика

Химическая термодинамика изучает энергетические эффекты реакций, их направ­ление и пределы самопроизвольного протекания.

Объект изучения в химической термодинамике — термодинамическая система (в дальнейшем просто система) — это совокупность взаимодействующих веществ, мысленно или реально обособленная от окружающей среды.

Система может находиться в различных состояниях. Состояние системы определяется численными значениями термодинамических параметров: температуры, давления, концен­траций веществ и пр. При изменении значения хотя бы одного из термодинамических параметров, например, температуры происходит изменение состояния системы. Изменение состояния системы называется термодинамическим процессом или просто процессом.

Процессы могут протекать с различными скоростями. В зависимости от условий перехода системы из одного состояния в другое, в химической термодинамике различают несколько типов процессов, простейшими из которых являются изо­термический, протекающий при постоянной температуре (Т=соnst), изобарный, протекающий при постоянном давлении (р=соnst), изохорный, протекающий при постоянном объёме (V=соnst) и адиабатический, который осуществляется без обмена теплотой между системой и окружающей средой (q=соnst). Наиболее часто в химической термодинамике реакции рассматриваются как изобарно-изотермические (р=соnst, Т=соnst) или изохорно-изотермические (V=соnst, Т=соnst) процессы.

Чаще всего в химической термодинамике рассматриваются реакции, притекающие в стандартных условиях, т.е. при стандартной температуре и стандартном состоянии всех веществ. В качестве стандартной принята температура 298К. Стандартным состоянием вещества является его состояние при давлении 101,3 кПа. Если вещество находится в растворе, за стан­дартное принимается его состояние при концентрации 1 моль/л.

Для ха­рактеристики процессов химическая термодинамика оперирует особыми величинами, называе­мыми функциями состояния: U – внутренняя энергия, Н – энтальпия, S – энтропия, G – энергия Гиббса и F – энергия Гельмгольца. Количественными характеристиками любого процесса являются изменения функций состояния, которые и определяются методами химической термодинамики:? ΔU, ΔH, ΔS, ΔG, ΔF.

Термохимический расчёт заключается в определении теплового эффекта реакции (теплоты реакции). Теплотой реакции, называется количество выделенной или поглощённой теплоты q. Если в ходе реакции теплота выделяется, такая реакция называется экзотермической, если теплота, поглощается, реакция называется эндотермической.

Численное значение теплоты реакции зависит от способа её проведения. В изохорном процессе, проводимом при V=соnst, теплота реакции q _V = Δ U, в изобарном процессе при р = соnst тепловой эффект q _p = Δ H. Таким образом, термохимический расчёт заключается в определении величины изменения или внутренней энергии, или энтальпии в ходе реакции. Поскольку подавляющее большинство реакций протекает в изобарных условиях (например, это все реакции в открытых сосудах, протекающие под атмосферным давлением), при проведении термохимических расчётов практически всегда производится расчёт ΔН. Если Δ Н<0, то реакция экзотермическая, если же Δ Н>0, то реакция эндотермическая.

Термохимические расчёты производятся, используя следствие из закона Гесса: тепловой эффект реакции равен сумме теплот (энтальпий) образования продуктов реакции за вычетом суммы теплот (энтальпий) образования реагентов.

Запишем в общем виде уравнение реакции: аА + bВ = сС + dD. Согласно следствию из закона Гесса теплота реакции определяется по формуле:

Δ Н = (c Δ Н _{обр, С} + d Δ Н _обр,_D) - (а Δ Н _обр,А + b Δ Н _обр,В), гдеΔ Н — теплота реакции; ΔН обр – теплоты (энтальпии) образования, соответственно, продуктов реакции С и D и реагентов А и В; с, d, а, b – коэффициенты в уравнении реакции, называемые стехиометрическим и коэффициентами.

Базовыми величинами в данной формуле являются теплоты (энтальпии) образования реагентов и продуктов. Теплотой (энтальпией) образования соединения называется тепловой эффект реакции, в ходе которой образуется 1 моль этого соединения из простых веществ, находящихся в термодинамически устойчивых фазах и модификация. Например, теплота образования воды в парообразном состоянии равна половине теплоты реакции, выражаемой уравнением: 2Н₂(г) + О₂(г) = 2Н₂О (г). Размерность теплоты образования – кДж/моль.

В термохимических расчётах теплоты реакций, как правило, определяются для стандартных условий, для которых формула приобретает вид: ΔН^°₂₉₈ = (cΔН^°_{298 обр С} + dΔН^°_{298 обр D}) - (аΔН^°_{298 о6р A} + bΔН^°_{298 обр В}), где ΔН°₂₉₈ – стандартная теплота реакции в кДж (стандартность величины указывается верхним индексом ^"О") при температуре 298К, а ΔН°_{298 обр}. — стандартные теплоты (энтальпии) образования соединений также при температуре 298К. Значения ΔН°_298обр. определены для всех соединений и являются табличными данными.

Энергией Гиббса реакции называется изменение энергии Гиббса Δ G при протекании химической реакции. Так как энергия Гиббса системы G = Н – ТS, её изменение в процессе определяется по формуле: Δ G = Δ Н – Т Δ S, где Т – абсолютная температура, К.

Энергия Гиббса химической реакции характеризует возможность её самопроизвольного протекания при постоянном давлении и температуре ( при р=соnst, Т=соnst). Если Δ G < 0, то реакция может протекать самопроизвольно, при Δ G > 0 самопроизвольное протекание реакции невозможно, если Δ G = 0, система находится в состоянии равновесия.

Для расчёта энергии Гиббса реакции отдельно определяются ΔН и ΔS. При этом в большинстве случаев используется слабая зависимость величин изменения энтальпии ΔН и энтропии ΔS от условий протекания реакции, т.е. пользуются приближениями: ΔН = ΔН°₂₉₈ и ΔS = ΔS°₂₉₈.

Стандартную теплоту реакции ΔН°₂₉₈ определяют, используя следствие из закона Гесса, а стандартную энтропию реакции аА + bВ = сС + dD рассчитывают по формуле: ΔS°₂₉₈= (сS°_{298 обрС} + dS°_{298, обрD}) – (aS°_{298 обрА} + bS°_298обрB), где ΔS°₂₉₈ – табличные значения абсолютных стандартных энтропии соединений в Дж/(мольК), а ΔS°₂₉₈ – стандартная энтропия реакции в Дж/К.

Если реакция протекает в стандартных условиях при температуре 298К, расчёт её энергии Гиббса (стандартной энергии Гиббса реакции) можно производить аналогично расчёту стандартной теплоты реакции по формуле, которая для реакции, выраженной уравнением аА + bВ = сС + dD, имеет вид:

ΔG ° ₂₉₈=(сΔG ° _{298 С} + dΔG ° _{298 D}) – (аΔG ° _{298 A} + bΔG ° _{298 B}), где ΔG ° ₂₉₈ — стандартная энергия Гиббса образования соединения в кДж/моль (табличные значения) – энергия Гиббса реакции, в которой при температуре 298К образуется 1 моль данного соединения, находящегося в стандартном состоянии, из простых веществ, также находящихся в стандартном состоянии, а ΔG ° ₂₉₈ – стандартная энергия Гиббса реакции в кДж.

Задача 1. Для данной реакции 2SO₂ (г)+ O₂(г) = 2SO₃(г) рассчитайте изменение энтальпии ΔН₂₉₈, энтропии ΔS₂₉₈ и энергии Гиббса ΔG₂₉₈. Рассчитайте температурную область самопроизвольного протекания реакции. Рассчитайте константу равновесия данной реакции при стандартных условиях (таблицы стандартных термодинамических потенциалов приводятся в различных справочниках).

Расчет энтальпии (ΔН₂₉₈^°):

_ΔН^°₂₉₈=Σ _ΔН_{продуктов реакции} – Σ _ΔН_{реагентов}

из приложения Таблицы стандартных термодинамических потенциалов выбираем значения _ΔН^°₂₉₈ для веществ, участвующих в реакции и подставляем их в расчетную формулу:

_ΔН^°₂₉₈=Σ _ΔН_{продуктов реакции} – Σ _ΔН_{реагентов}= 2? _ΔН₂₉₈^° (SO₃)–(2? _ΔН₂₉₈^°(SO₂) +_ΔН₂₉₈^° (O₂))= =2 (−395,2) −(2 (−296,9) + 0) = − 197,2 кДж/моль

Расчет энтропии (ΔS^°₂₉₈):

ΔS^°₂₉₈=Σ _ΔS_{продуктов реакции} – Σ _ΔS_{реагентов}

из таблицы стандартных термодинамических потенциалов выбираем значения ΔS^°₂₉₈ для веществ, участвующих в реакции и подставляем их в расчетную формулу:

ΔS^°₂₉₈=Σ _ΔS_{продуктов реакции} – Σ _ΔS_{реагентов} =2? ΔS^°₂₉₈ (SO₃) -(2?ΔS^°₂₉₈ (SO₂)+ ΔS^°₂₉₈ (О₂)) =

=2? 256,2 – (2?248,1 +205) = –188,8 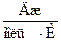= –0,1888 .

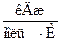Расчет энергии Гиббса (_ΔG^°₂₉₈):

_ΔG^°₂₉₈= _ΔН^°₂₉₈ – T? ΔS^°₂₉₈

по полученным данным рассчитываем энергию Гиббса (при стандартных условиях Т = 298К):

_ΔG^°₂₉₈=_ΔН^°₂₉₈–T?ΔS^°₂₉₈=−197,2кДж/моль – 298?(–0,1888) 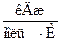= –140,9 кДж/моль.

Расчет показывает, что окисление диоксида серы кислородом при 25ºC (298K) термодинамически возможный процесс (т.к.?G<0). В ходе этой реакции энтропия уменьшается и, следовательно, с ростом температуры уменьшается возможность протекания этой реакции.

Определение температурной области самопроизвольного протекания реакции.

Так как условием самопроизвольного протекания реакции является отрицательность DG (DG<0), определение области температур, в которой реакция может протекать самопроизвольно, сводится к решению неравенства (DH–TDS)

Реакция протекает самопроизвольно, если _ΔG^°₂₉₈≤ 0, следовательно:

_ΔН^°₂₉₈– T? _ΔS^°₂₉₈ ≤ 0, отсюда 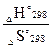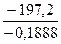Т ≤ ≤ ; Т ≤ 1044,5 К (771,5?С),

т.е. при всех температурах, меньших 1044,5 К, будет обеспечиваться отрицательность DG и, следовательно, в данном температурном диапазоне будет возможным самопроизвольное протекание рассматриваемой реакции.

Расчет константы химического равновесия:

Кр = e 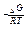, где R=8,31 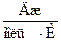=0,00831 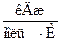, Т = 298К.

Рассчитываем, используя известные данные:

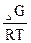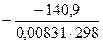– = = 56,9;

Кр = e ^56,9 = 5,14·10²⁴