Погрешность приближенного решения во многих задачах, когда одним из определяющих параметров алгоритма является положительная величина 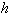 - шаг сетки, можно записать в виде:
- шаг сетки, можно записать в виде:
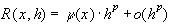 (27)
(27)
В частности, в таком виде записываются формулы (23) и (26) для погрешностей приближенного дифференцирования со значениями 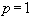 и
и 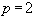 .
.
На сетке с шагом 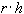 при конечном
при конечном 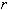 имеем:
имеем:
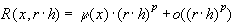 (28)
(28)

Пренебрегая в формулах (27) и (28) величинами  (т.е. рассматривая только старший член погрешности), из (1) и (2) находим:
(т.е. рассматривая только старший член погрешности), из (1) и (2) находим:
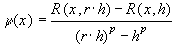 (29)
(29)
Так как 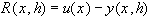 , где
, где  - точное значение искомой величины, а
- точное значение искомой величины, а  ее приближение, полученное на сетке с шагом
ее приближение, полученное на сетке с шагом 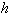 , то из (29) получаем
, то из (29) получаем
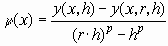 (30)
(30)
а подставив это в (27), получаем приближенную формулу для погрешности, которая называется первой формулой Рунге:
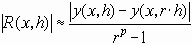 (31)
(31)
Эта формула дает величину погрешности с точностью до членов порядка  .
.
Принципиальное отличие этой формулы от оценок погрешности типа 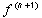 ,
, 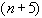 в том,что формула Рунге использует только полученные приближенные решения и не требует оценок каких-либо величин исходной задачи. Чаще всего на практике отношение шагов сетки
в том,что формула Рунге использует только полученные приближенные решения и не требует оценок каких-либо величин исходной задачи. Чаще всего на практике отношение шагов сетки 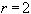 .
.
 2015-01-30
2015-01-30 296
296







