2015-01-30
211
Пусть 
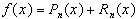(18)
Дифференцируя формулу (18) m раз, получаем:
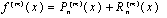(19)
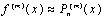(20)
Рассматривая интерполяционный многочлен в форме Ньютона и используя обозначения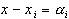 
, имеем
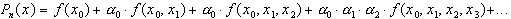
Тогда
...
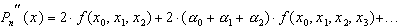
Оставляя в правых частях полученных формул только первые слагаемые, можно записать следующие простые приближенные выражения для производных:
................................................
Пусть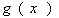 
- достаточно гладкая функция.
Исследуем погрешность приближенных формул для производных первого и второго порядка.
Пусть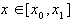 
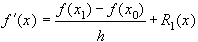(21)
где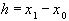 
, 
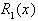- погрешность.
Заменяя значение функции в точке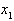 
по формуле Тейлора
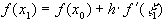, где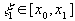 
,
получаем
.
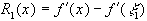Еще раз применяя формулу Тейлора, получаем
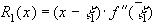, где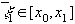 
.
Таким образом, если функция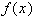 
имеет ограниченную производную второго порядка, то погрешность в формуле (21) для любого 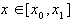оценивается неравенством
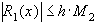(22)
где 
, и при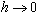 
.
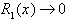В случае, когда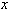 
совпадает с одним из узлов интерполяции 
или 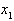, можно получить больше информации о погрешности приближенного решения. Пусть 
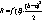. Используя формулу Тейлора
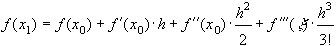
из (21) получаем
.
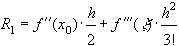При 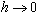величина 
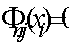(если третья производная функции 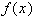ограничена) бесконечно малая величина порядка 
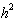, т.е.
|
|
|
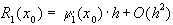(23)
где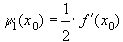 
.
Формулу приближенного вычисления второй производной функции 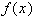рассмотрим для важного частного случая, когда 
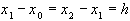. Возьмем 
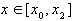. Тогда ее можно записать в виде
(24)
По формуле Тейлора
, 
, 
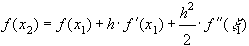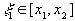
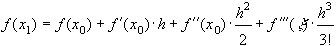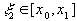
Подставляя эти выражения, получаем
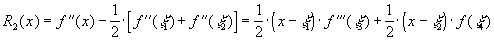
Таким образом, если функция 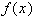имеет ограниченную производную третьего порядка, то погрешность формулы (24) для произвольной точки 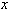оценивается следующим образом:
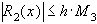(25)
где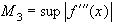 
.
Если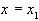 
, то используя для значени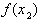й 
и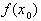 
формулу Тейлора, заканчивающуюся членом с производной 4 - го порядка, получаем для погрешности выражение
.
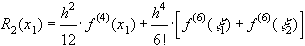Таким образом, если функция имеет ограниченную производную 6-го порядка, то
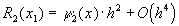(26)
