Пример 1. Кинетическая энергия электрона в атоме порядка 10,0 эВ. Используя соотношения неопределенностей, определить: 1) минимальные линейные размеры атома; 2) естественную ширину Dl спектральной линии излучения атома при переходе его из возбужденного состояния в основное. Среднее время t жизни атома в возбужденном состоянии принять равным 1,00·10-8 с, а длину волны l излучения равной 600 нм.
Решение. 1. Неопределенность координаты и импульса электрона связаны соотношением
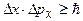 , (1)
, (1)
где 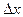 - неопределенность координаты электрона;
- неопределенность координаты электрона; 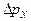 - неопределенность его импульса.
- неопределенность его импульса.
2. Пусть атом имеет линейные размеры 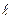 , тогда электрон атома будет находиться где-то в пределах области с неопределенностью
, тогда электрон атома будет находиться где-то в пределах области с неопределенностью 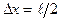 . Соотношение (1) можно записать в этом случае в виде
. Соотношение (1) можно записать в этом случае в виде 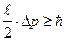 , откуда
, откуда
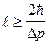 . (2)
. (2)
3. Физически разумная неопределенность импульса 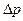 не должна превышать значения самого импульса p, т.е.
не должна превышать значения самого импульса p, т.е.
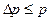 .
.
4. Импульс p связан с кинетической энергией T соотношением 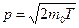 . Заменим
. Заменим 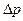 значением
значением 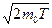 (такая замена не увеличит
(такая замена не увеличит 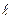 ). Переходя от неравенства (2) к равенству, получим
). Переходя от неравенства (2) к равенству, получим 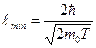 . Подставив числовые значения, найдем:
. Подставив числовые значения, найдем:
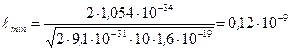 м.
м.
5. При переходе атомов из возбужденного состояния в основное существует некоторый разброс (неопределенность) в энергии испускаемых фотонов. Это связано с тем, что энергия возбужденного состояния не является точно определенной, а имеет конечную ширину 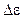 . Согласно соотношению неопределенностей энергии и времени, ширина
. Согласно соотношению неопределенностей энергии и времени, ширина 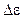 энергетического уровня возбужденного состояния связана со средним временем жизни атомов в этом состоянии соотношением:
энергетического уровня возбужденного состояния связана со средним временем жизни атомов в этом состоянии соотношением:
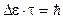 .
.
6. Вследствие конечной ширины уровня энергии возбужденного состояния энергия фотонов, испускаемых атомами, также имеет разброс, равный ширине энергетического уровня. Тогда
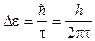 . (3)
. (3)
7. Энергия фотона e связана с длиной волны l соотношением:
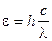 . (4)
. (4)
8. Чтобы найти Dl, продифференцируем соотношение (4) по l и заменим бесконечно малые приращения соответствующих величин на конечные:
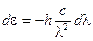 ,
, 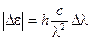 . (5)
. (5)
В этом выражении конечный интервал длин волн  есть естественная ширина спектральной линии.
есть естественная ширина спектральной линии.
9. Выразив  из формулы (5) и заменив
из формулы (5) и заменив 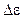 согласно (3), получим
согласно (3), получим
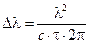 .
.
10. Произведем вычисления
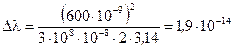 м.
м.
Ответ: 1) 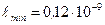 м;
м;
2) 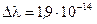 м.
м.
Пример 2. Электрон находится в бесконечно глубоком одномерном прямоугольном потенциальном ящике шириной 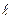 . Определить: 1) вероятность того, что электрон, находящийся в возбужденном состоянии (
. Определить: 1) вероятность того, что электрон, находящийся в возбужденном состоянии (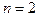 ), будет обнаружен в средней трети ящика; 2) в каких точках интервала (
), будет обнаружен в средней трети ящика; 2) в каких точках интервала (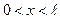 ) плотность вероятности
) плотность вероятности 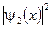 нахождения частицы максимальна и минимальна?
нахождения частицы максимальна и минимальна?
Решение. 1. Вероятность W обнаружить частицу в интервале 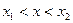 определяется интегралом
определяется интегралом
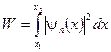 , (1)
, (1)
где 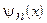 - нормированная собственная волновая функция, описывающая состояние электрона в потенциальном ящике, которая имеет вид:
- нормированная собственная волновая функция, описывающая состояние электрона в потенциальном ящике, которая имеет вид:
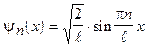 .
.
2. Возбужденному состоянию (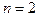 ) отвечает собственная волновая функция:
) отвечает собственная волновая функция:
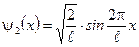 . (2)
. (2)
3. Подставив 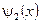 в подынтегральное выражение формулы (1) и вынося постоянные величины за знак интеграла, получим:
в подынтегральное выражение формулы (1) и вынося постоянные величины за знак интеграла, получим:
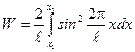 . (3)
. (3)
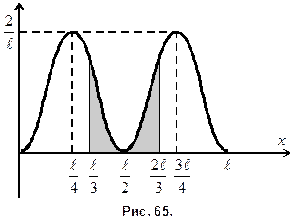 4. Согласно условию задачи
4. Согласно условию задачи 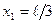 и
и 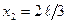 (рис. 65). Подставим эти пределы интегрирования в формулу (3) и произведем замену
(рис. 65). Подставим эти пределы интегрирования в формулу (3) и произведем замену
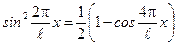 .
.
Разобьем интеграл на два:

5. Заметив, что 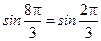 , а
, а 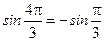 , получим
, получим
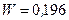 .
.
6. Плотность вероятности 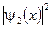 для рассматриваемого случая определяется выражением
для рассматриваемого случая определяется выражением
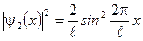 .
.
7. Для удобства дальнейших преобразований введем обозначение: 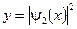 . Тогда
. Тогда 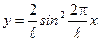 . Проведем исследование этой функции на экстремумы. Возьмем первую производную y по x, приравняем полученное выражение к нулю. Решив полученное уравнение, найдем значения x, отвечающие экстремумам y:
. Проведем исследование этой функции на экстремумы. Возьмем первую производную y по x, приравняем полученное выражение к нулю. Решив полученное уравнение, найдем значения x, отвечающие экстремумам y:
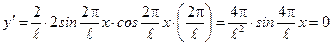 ;
;
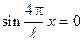 ;
; 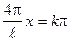 ;
; 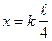 , где
, где 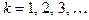
8. Координаты экстремумов: 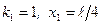 ;
; 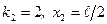 ;
; 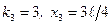 .
.
9. Максимум или минимум имеет функция при найденных значениях 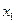 ,
, 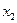 и
и 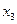 , необходимо установить знак второй производной
, необходимо установить знак второй производной 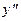 при значениях
при значениях 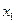 ,
, 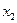 и
и 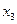 :
:
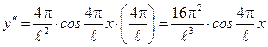 .
.
· 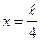 ;
; 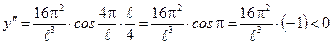 .
.
· 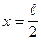 ;
; 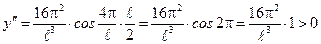 .
.
· 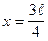 ;
; 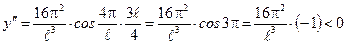 .
.
10. Следовательно, в точках 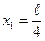 и
и 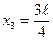 плотность вероятности
плотность вероятности 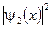 будет максимальна, а в точке
будет максимальна, а в точке 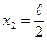 - минимальна (рис. 65).
- минимальна (рис. 65).
Ответ: 1) 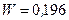 ;
;
2) Координаты максимумов:
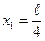 и
и 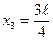 .
.
Координата минимума 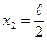 .
.
Пример 3. Кусок металла (медь) объема 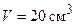 находится при температуре
находится при температуре 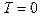 . Определить: 1) максимальную энергию
. Определить: 1) максимальную энергию 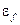 (энергию Ферми), которую могут иметь свободные электроны в металле при
(энергию Ферми), которую могут иметь свободные электроны в металле при 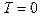 , приняв, что на каждый атом меди приходится по одному электрону; 2) долю свободных электронов, энергии которых заключены в интервале от
, приняв, что на каждый атом меди приходится по одному электрону; 2) долю свободных электронов, энергии которых заключены в интервале от 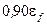 до
до 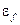 ; 3) среднюю кинетическую энергию
; 3) среднюю кинетическую энергию 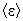 свободных электронов.
свободных электронов.
Решение. 1. Максимальная кинетическая энергия 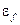 , которую могут иметь электроны в металле при абсолютном нуле, связана с концентрацией свободных электронов соотношением:
, которую могут иметь электроны в металле при абсолютном нуле, связана с концентрацией свободных электронов соотношением:
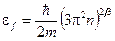 , (1)
, (1)
где 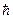 - постоянная Планка, деленная на 2p; m - масса электрона.
- постоянная Планка, деленная на 2p; m - масса электрона.
2. Концентрация свободных электронов по условию задачи равна концентрации атомов, которая может быть найдена по формуле:
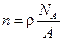 ,
,
где r - плотность меди; 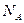 - число Авогадро; A - масса килоатома.
- число Авогадро; A - масса килоатома.
3. Подставляя выражение концентрации в формулу (1), получаем:
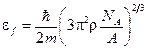 .
.
4. Подставив числовые значения, произведем вычисления:
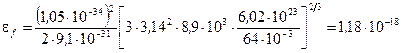 Дж = 7,4эВ.
Дж = 7,4эВ.
5. Число электронов в единице объема, энергии которых заключены в интервале от 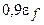 до
до 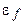 , найдем интегрированием:
, найдем интегрированием:
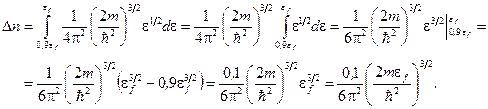
6. После подстановки числовых значений получим:
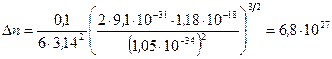 эл/м3.
эл/м3.
7. Для определения средней кинетической энергии 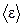 свободных электронов воспользуемся известным соотношением
свободных электронов воспользуемся известным соотношением
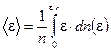 .
.
8. Подставив функциональную зависимость 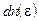 и выполнив преобразования, получим:
и выполнив преобразования, получим:
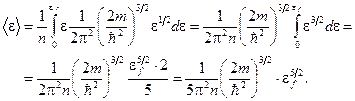 (2)
(2)
9. Учитывая, что 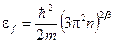 , запишем
, запишем
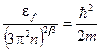 .
.
10. Объединив с выражением (2), получим:
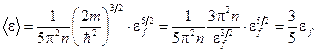 .
.
11. Подставляя в последнюю формулу численное значение, найдем среднюю энергию
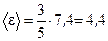 эВ.
эВ.
Ответ: 1) 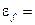 1,18·10-18 Дж = 7,4 эВ;
1,18·10-18 Дж = 7,4 эВ;
2) 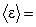 4,4 эВ.
4,4 эВ.
Пример 4. Рассчитать ширину запрещенной зоны 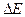 носителей тока в теллуре, если при нагревании от
носителей тока в теллуре, если при нагревании от 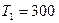 К до
К до 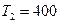 К его проводимость возрастает в 5,00 раз.
К его проводимость возрастает в 5,00 раз.
Решение. 1.Теллур является полупроводником, его собственная проводимость s зависит от температуры T по закону
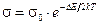 , (1)
, (1)
где 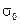 - величина, слабо меняющаяся с температурой;
- величина, слабо меняющаяся с температурой; 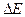 - ширина запрещенной зоны; k - постоянная Больцмана.
- ширина запрещенной зоны; k - постоянная Больцмана.
2. Используя соотношение (1), запишем проводимость теллура при температурах 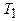 и
и 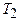 :
:
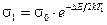 ; (2)
; (2)
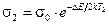 ; (3)
; (3)
3. Разделив выражение (3) на (2), имеем:
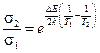 .
.
4. После логарифмирования  , выразим ширину запрещенной зоны
, выразим ширину запрещенной зоны
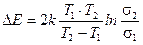 .
.
5. Подставим числовые значения:
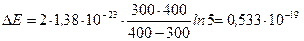 Дж = 0,333эВ.
Дж = 0,333эВ.
Ответ: 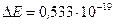 Дж = 0,333эВ.
Дж = 0,333эВ.
Пример 5. Определить начальную активность 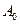 радиоактивного магния
радиоактивного магния 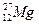 массой
массой 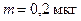 , а также активность A по истечении времени
, а также активность A по истечении времени 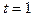 ч. Предполагается, что все атомы изотопа радиоактивны.
ч. Предполагается, что все атомы изотопа радиоактивны.
Решение. 1. Начальная активность изотопа:
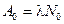 , (1)
, (1)
где l - постоянная радиоактивного распада; 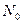 - количество атомов изотопа в начальный момент (
- количество атомов изотопа в начальный момент (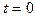 ).
).
2. Учтем, что 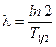 ,
, 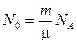 , тогда формула (1) примет вид
, тогда формула (1) примет вид
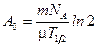 . (2)
. (2)
3. Выразим входящие в эту формулу величины в СИ и произведем вычисления:
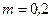 мг = 0,2·10-9кг;
мг = 0,2·10-9кг; 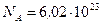 моль-1;
моль-1;
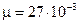 кг/моль;
кг/моль; 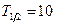 мин = 600с.
мин = 600с.
4. Активность изотопа уменьшается со временем по закону:
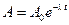 . (3)
. (3)
5. Заменив в формуле (3) постоянную распада l ее выражением, получим:
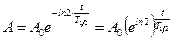 .
.
6. Так как 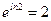 , то окончательно будем иметь:
, то окончательно будем иметь:
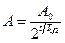 .
.
7. Сделав подстановку числовых значений, получим:
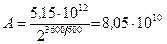 Бк.
Бк.
Ответ: 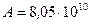 Бк.
Бк.
Пример 6. Найти энергию реакции 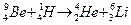 .
.
Решение. 1. Определим энергию реакции:
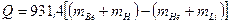 МэВ.
МэВ.
2. При числовом подсчете массы ядер заменим массами нейтральных атомов:
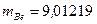 а.е.м.;
а.е.м.;
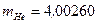 а.е.м.;
а.е.м.;
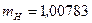 а.е.м.;
а.е.м.;
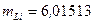 а.е.м.
а.е.м.
3. Подставим значения масс в формулу и получим Q:
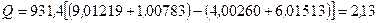 МэВ.
МэВ.
Ответ: 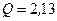 МэВ.
МэВ.
Пример 7. Вычислить толщину слоя половинного ослабления 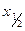 параллельного пучка
параллельного пучка 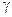 -излучения для воды, если линейный коэффициент ослабления
-излучения для воды, если линейный коэффициент ослабления 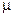 = 0,047 см-1.
= 0,047 см-1.
Решение. 1. При прохождении g-излучений через слой вещества происходит их поглощение за счет трех факторов: фотоэффекта, эффекта Комптона и образования пар (электрон-позитрон). В результате действия этих трех факторов интенсивность g-излучения экспоненциально убывает в зависимости от толщины слоя:
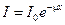 . (1)
. (1)
2. Пройдя поглощающий слой толщиной, равной толщине слоя половинного ослабления 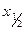 , пучок g-излучения будет иметь интенсивность
, пучок g-излучения будет иметь интенсивность 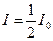 . Подставив значения
. Подставив значения 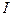 и х в формулу (1), получим
и х в формулу (1), получим
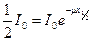 . (2)
. (2)
После сокращения на 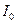 уравнение (2) примет вид
уравнение (2) примет вид
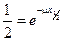 . (3)
. (3)
3. Прологарифмируем выражение (3)
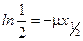 . (4)
. (4)
4. Найдем искомое значение толщины слоя половинного ослабления
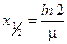 . (5)
. (5)
5. Подставим в формулу (5) значения 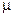 и
и 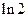 , найдем величину
, найдем величину 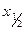 :
:
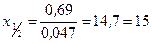 см.
см.
Вывод - слой воды толщиной в 15 см снижает интенсивность g-излучения в два раза.
Ответ: 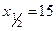 см.
см.
Пример 8. Радиоактивный точечный источник 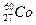 находится в центре свинцового сферического контейнера с внешним радиусом R = 20,0см и с толщиной стенок х = 1,00см. Определить максимальную активность
находится в центре свинцового сферического контейнера с внешним радиусом R = 20,0см и с толщиной стенок х = 1,00см. Определить максимальную активность 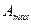 источника, который можно хранить в контейнере, при допустимой плотности потока,
источника, который можно хранить в контейнере, при допустимой плотности потока, 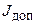 g-фотонов с внешней стороны контейнера равной 8,00·106 (с-1·м-2). Принять, что при каждом акте распада ядра
g-фотонов с внешней стороны контейнера равной 8,00·106 (с-1·м-2). Принять, что при каждом акте распада ядра 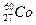 испускается п = 2 g-фотона, средняя энергия которых
испускается п = 2 g-фотона, средняя энергия которых 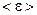 = 1,25 МэВ.
= 1,25 МэВ.
Р е ш е н и е. 1. Активность радиоактивного источника пропорциональна потоку излучения g-фотонов
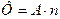 , (1)
, (1)
где п - число g-фотонов, испускаемых при одном акте распада.
2. Найдем из уравнения (1) активность
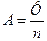 . (2)
. (2)
3. Выразим поток Ф, входящий в формулу (2), через плотность потока 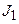 , который на расстоянии R от точечного источника излучений равен
, который на расстоянии R от точечного источника излучений равен
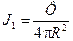 . (3)
. (3)
4. После прохождения излучения через свинцовую стенку контейнера плотность потока уменьшится и будет равна
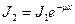 . (4)
. (4)
5. Найдем из (4) плотность потока 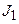 и подставим в формулу (3), в результате получим равенство
и подставим в формулу (3), в результате получим равенство
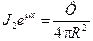 , (5)
, (5)
откуда получим выражение для потока
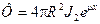 . (6)
. (6)
6. Подставим выражение (6) для потока Ф в (2) и определим активность А препарата
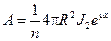 . (7)
. (7)
7. Если заменить в полученной формуле 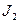 на
на 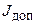 , то формула (7) будет выражать искомую максимальную активность источника, который можно хранить в контейнере:
, то формула (7) будет выражать искомую максимальную активность источника, который можно хранить в контейнере:
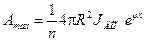 . (8)
. (8)
8. По графику (см. приложение табл. 9) найдём линейный коэффициент ослабления 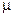 для
для 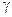 -фотонов с энергией
-фотонов с энергией 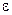 = 1,25 МэВ, который равен 0,64 см-1.
= 1,25 МэВ, который равен 0,64 см-1.
9. Выразим величины, входящие в формулу (8), в единицах СИ, выполним вычисления и получим искомую активность
 МБк.
МБк.
Вывод: Данный контейнер предназначен для хранения g-радиоактивных источников с активностью не превышающей 3,81 МБк.
Ответ: 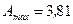 МБк.
МБк.
Пример 9. Космическое излучение на уровне моря на экваторе образует в воздухе объемом V = 1,0 см3 в среднем N = 24 пары ионов за время 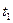 = 10 с. Определить экспозиционную дозу X, получаемую человеком за время
= 10 с. Определить экспозиционную дозу X, получаемую человеком за время 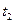 = 1,0 год.
= 1,0 год.
Р е ш е н и е. 1. Экспозиционную дозу, получаемую человеком, можно определить по формуле
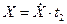 , (1)
, (1)
где 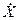 - мощность экспозиционной дозы излучения.
- мощность экспозиционной дозы излучения.
2. Мощность дозы
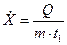 , (2)
, (2)
где 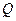 - заряд ионов одного знака, образуемых излучением за время
- заряд ионов одного знака, образуемых излучением за время 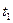 в воздухе массой т.
в воздухе массой т.
3. Найдем массу воздуха из его плотности 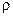 и занимаемого объема
и занимаемого объема 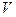 :
:
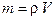 . (3)
. (3)
4. Заряд всех ионов одного знака найдем равен
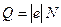 . (4)
. (4)
5. Подставим в формулу (1) выражения для мощности дозы 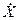 (2), массы
(2), массы 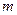 (3) и электрического заряда
(3) и электрического заряда 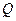 (4) и получим расчетную формулу
(4) и получим расчетную формулу
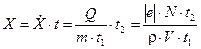 . (5)
. (5)
6. Подставим величины, входящие в формулу (5), в единицах СИ и выполним вычисления
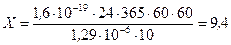 мкКл/кг.
мкКл/кг.
Вывод: Экспозиционная доза, получаемая человеком за счет космического излучения в год равна 9,4 мкКл/кг.
Ответ: 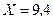 мкКл/кг.
мкКл/кг.
 2015-01-30
2015-01-30 2702
2702
