В задачах 1 – 4 проверить, что следующие множества являются линейными векторными пространствами.
1. Множество R3 всех геометрических векторов.
2. Множество Rn всех арифметических n-компонентных векторов 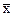 = (х1, x2, …, xn).
= (х1, x2, …, xn).
3. Множество Pn всех многочленов
P (t) = a n-1 tn-1 + … + a 1 t + a 0
степени £ n – 1 с естественным образом введенными операциями сложения многочленов и умножения их на число.
4. Множество Мm, n всех матриц размерности m x n.
В задачах 5 – 9 выяснить, являются ли следующие множества линейными векторными пространствами:
5. Множество R1 всех геометрических векторов, коллинеарных фиксированной прямой.
6. Множество R2 всех геометрических векторов, исходящих из начала координат, концы которых лежат на фиксированной прямой у = kx + b.
7. Множество всех геометрических векторов, удовлетворяющих условию | 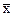 | > a, где а > 0 – фиксированное число.
| > a, где а > 0 – фиксированное число.
8. Множество всех сходящихся последовательностей.
9. Множество всех функций, интегрируемых на отрезке
[ a, b].
Ответ. 5) да; 6) да, если b= 0; нет, если b ¹ 0; 7) нет;
8) да; 9) да.
В задачах 10 – 12 в произвольном пространстве Ln векторы 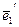 ,
,  , …,
, …, 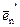 и
и 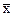 заданы своими координатами в некотором базисе В. Доказать, что система В¢ = (
заданы своими координатами в некотором базисе В. Доказать, что система В¢ = (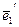 ,
,  , …,
, …, 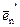 ) – базис, и найти координаты вектора
) – базис, и найти координаты вектора 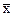 в базисе В¢.
в базисе В¢.
10. 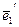 =
=  + 2
+ 2  ,
,  =
=  ,
, 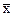 = 5
= 5  + 6
+ 6  .
.
11. 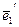 =
=  +
+  +
+ 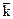 ,
,  =
=  +
+  + 2
+ 2 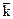 ,
, 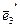 =
=  + 2
+ 2  + 3
+ 3 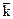 ,
,
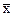 = 6
= 6  + 3
+ 3  + 14
+ 14 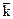 .
.
12. 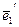 = 2
= 2  +
+  - 3
- 3 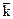 ,
,  = 3
= 3  + 2
+ 2  - 5
- 5 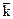 ,
, 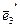 =
=  -
-  +
+ 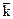 ,
,
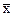 = 6
= 6  + 2
+ 2  - 7
- 7 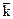 .
.
Ответ. 10) Х¢ = 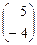 ; 11) Х¢ =
; 11) Х¢ = 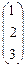 ; 12) Х¢ =
; 12) Х¢ = 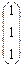 .
.
В задачах 13 – 14 даны два линейных преобразования. Найти матрицу линейного преобразования, выражающего вектор 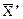 через вектор
через вектор 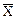 :
:
13. 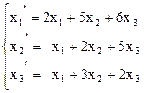 ,
, 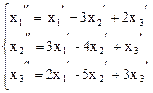
14. 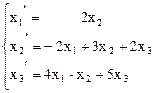 ,
, 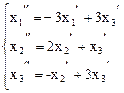
Ответ. 13) 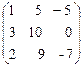 , 14)
, 14) 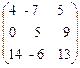 .
.
Пусть В = ( ,
,  ) и В¢ = (
) и В¢ = ( ¢,
¢,  ¢) – прямоугольные базисы в R2. В задачах 15 – 20 найти матрицу перехода ТВ®В¢ (матрицу линейного преобразования).
¢) – прямоугольные базисы в R2. В задачах 15 – 20 найти матрицу перехода ТВ®В¢ (матрицу линейного преобразования).
15. Базис В¢ получен изменением на противоположное направление всех базисных ортов В.
16. Базис В¢ получен перестановкой базисных ортов В.
17. Базис В¢ получен растяжением вектора  в k раз.
в k раз.
18. Базис В¢ получен растяжением базисных ортов В в k раз.
19. Базис В¢ получен зеркальным отображением от вектора  .
.
20. Базис В¢ получен поворотом базиса В на угол a
(a ¹ 0, a ¹ p).
Ответ. 15) 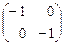 , 16)
, 16) 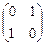 , 17)
, 17) 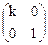 ,
,
18) 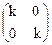 , 19)
, 19) 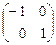 , 20)
, 20) 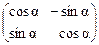 .
.
 2015-01-07
2015-01-07 2422
2422
