Повторение испытаний. Формула Бернулли. Приближенная формула Пуассона

Пусть производится n независимых испытаний, в каждом из к-рых событие А может появиться или не появится. Вер-ть события А в каждом испытании одинакова и =р. Вер-ть ненаступления события А=q=1-р.Вычислим вер-ть того, что при n испытаниях событие А осуществится ровно k раз.

Предположим, что событие А появилось в каждом из k испытаниях и не появилось в остальных n-k испытаниях. Т.к. исход испытания в каждом из n испытаний не зависит от результата в любом другом испытании, то вер-ть такого сложного события =произведению вер-тей, т.е.: =р^k·q^n-k

Число этих сложных событий=числу сочетаний из n эл-тов по k Эл-тов. Эти сложные события не совместны, поэтому вер-ть суммы этих событий = сумме их вер-тей, а т.к. все слогаемые равны между собой, то можно одно из них умножить на кол-во: 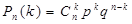(1) – ф. Бернулли

Примеры.

1. Реш-е: А – день дождливый

р=Р(А)=12/30=2/5; q=3/5;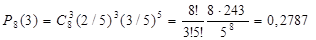

2. Реш-е: Вер-ть рождения М: р-1-q=1-0,482=0,518.

«не менее трех М»= «3М» и «4М» (события несовместны). Поэтому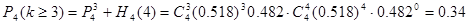

Замечание 1. Вер-ть Р_n(k) при данном n сначала ↑ при изменении 0≤k≤k0, а затем ↓ при изменении k от k₀ до n. Поэтому k₀ называется наивероятнейшим числом наступления успеха в n опытах. Это число k₀=целой части числа (n+1)·р, если число (n+1)·р – целое, то наивероятнейшим явл-ся также число k₀-1 с той же вер-тью Р_n(k).

Пример 3. Реш-е: k₀=(n+1)·р; n=7; p=2/3; k₀= 8·2/3=16/3=5

Замечание 2. В том случае, когда n велико, а p мало (р<0,1; npq≤9) вместо формулы Бернулли применяют приближенную формулу Пуассона:

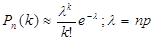Формула Пуассона исп-ся в задачах, относящихся к редким событиям.

Пример 4. Реш-е: р=0,001, n=5000; q=0,009; npq=5000·0,001·0,009=0,045<9; λ=5

Р₅₀₀₀(2≤k≤5000) -? Найдем вер-ти попадания в цель одной пули и ни одной:Р5₀₀₀(0)≈(50/0!)·е^-5≈е^-5

Р₅₀₀₀(1)≈5(1/1!)·е^-5≈5е^-5; Р₅₀₀₀(2≤k≤5000)≈1-е^-5-5е^-5=0,9596

13. Локальная и интегральная теоремы Лапласа. Вер-ть отклонения относительной частоты от постоянной вер-ти в независимых испытаниях.

При большом числе испытаний применение формулы Бернулли связано с большими вычислит.трудностями. Для этого случая исп-ся лок.теорема Лапласа. Для частного случая (р=1/2) приближенная (асимптотическая) была найдена Абрахом Муавром в 1730г. В 1783 Лаплас обощил формулу Муавра для произвольного р≠0 и ≠1. Поэтому теорему называют иногда т.Муавра-Лапласа.

Локк.теорема: Если вер-ть р появления события А в каждом испытании постоянна и отлична от 0 и 1, то вер-ть Р_n(k) того, что событие А появится в n испытаниях ровно k раз, приближенно равно (тем точнее, чем больше n) значениям ф-ции: 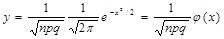при х=(k-np)/(npq)^1/2

Вер-ть: Р_n(k)≈(1/(npq)^1/2)·φ(х)

Пример 1. Реш-е: q=1-0,15=0,85,р=0,15,n=200,k=20

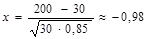По таблице:φ(х)≈0,0562=>Р₂₀₀(20)≈0,0562/(30·0,85)=1,112·10^-2

Итегр.теорема

Если при условиях лок.теоремы требуется вычислить вер-ть того, что событие появится не менее k₁ и не более k₂ раз, то решение этой задачи дает интегр.теорема Лапласа.

Теорема. Если вер-ть наступления события А в каждом испытании постоянна и ≠0 и ≠1, то вер-ть Рn(k₁,k₂) того, что событие А появится в испытаниях от k₁ до k₂ раз, приближенно равна определенному интегралу 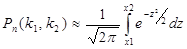, где х₁=(k₁-np)/(npq)^1/2; x₂=(k₂-np)/(npq)^1/2.

При вычислении интеграла нельзя воспользоваться формулой Ньютона-Лейбница, т.к. интеграл не выражается в элементарных ф-циях.

Для ф-ции 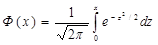, к-рая называется ф-цией Лапласа есть табл. Ф(-х)=-Ф(х)

Вер-ть: 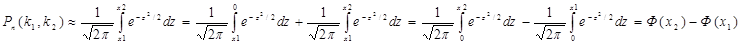Т.о. Рn(k₁,k₂)≈Ф(х2)-Ф(х1), где х₁=(k₁-np)/(npq)^1/2; x₂=(k₂-np)/(npq)^1/2.

Ф(х)-ф-ция Лапласа

Пример 2. Реш-е: р=0,12, q=0.88;n=500,k₁=0,k₂=50.

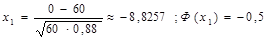
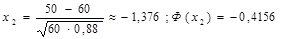
Замечание. Справедлива след. приближенная формула: Р(|(m/m)-р|≤ε)≈2Ф(ε·(n/pq)^1/2) – формула вер-ти отклонения относит.частоты от постоянной вер-ти в независимых испытаниях (m/n-относит.частоты)

Пример 3. Реш-е: Р(|(m/m)-0,5|≤ε)≈0,92=> 2Ф(0,01·√(n/0,5·0,5))≈0,92; Ф(0,02·√n) ≈0,46; 0,02·√n=1,74; √n=87; n=7569