Гипербола. Гиперболой называется геометрическое место точек на плоскости, разность расстояний которых до двух данных точек

Гиперболой называется геометрическое место точек на плоскости, разность расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная.

Каноническое уравнение гиперболы в выбранной системе координат имеет вид:

,

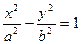где .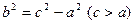

Вершины эллипса имеют следующие координаты:

.

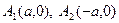Отрезок 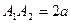- большая ось эллипса, отрезок 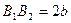- малая ось эллипса, соответственно 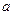и 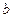- большая и малая полуоси эллипса.

Фокуса эллипса имеют следующие координаты:

.

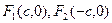Асимптоты гиперболы – это прямые 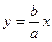и .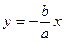

При 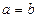гипербола называется равносторонней.

Замечание 1. Если мнимая ось гиперболы равна 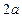и расположена на оси ОХ, а действительная ось равна 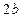и расположена на оси ОY, то уравнение такой гиперболы имеет вид:

.

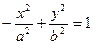Замечание 2. Эксцентриситетом гиперболы называется отношение фокусного расстояния к действительной оси:

.

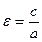Для любой гиперболы 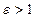, это число определяет форму гиперболы.