При расчете средней арифметической для интервального вариационного ряда сначала определяют среднюю для каждого интервала, как полусумму верхней и нижней границ, а затем — среднюю всего ряда. В случае открытых интервалов значение нижнего или верхнего интервала определяется по величине интервалов, примыкающих к ним.
Средние, вычисляемые из интервальных рядов являются приближенными.
Пример 3. Определить средний возраст студентов вечернего отделения.
| Возраст в годах!!х?? | Число студентов 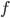 | Среднее значение интервала 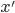 | Произведение середины интервала (возраст) на число студентов 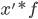 |
| до 20 | (18 + 20) / 2 =19 18 в данном случае граница нижнего интервала. Вычисляется как 20 — (22-20) | ||
| 20 — 22 | (20 + 22) / 2 = 21 | ||
| 22 — 26 | (22 + 26) / 2 = 24 | ||
| 26 — 30 | (26 + 30) / 2 = 28 | ||
| 30 и более | (30 + 34) / 2 = 32 | ||
| Итого |
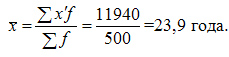
Средние, вычисляемые из интервальных рядов являются приближенными. Степень их приближения зависит от того, в какой мере фактическое распределение единиц совокупности внутри интервала приближается к равномерному.
При расчете средних в качестве весов могут использоваться не только абсолютные, но и относительные величины (частость):
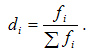
Средняя арифметическая обладает целым рядом свойств, которые более полно раскрывают ее сущность и упрощают расчет:
1. Произведение средней на сумму частот всегда равно сумме произведений вариант на частоты, т.е.
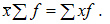
2.Средняя арифметическая суммы варьирующих величин равна сумме средних арифметических этих величин:
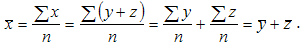
3.Алгебраическая сумма отклонений индивидуальных значений признака от средней равна нулю:
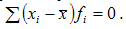
4.Сумма квадратов отклонений вариантов от средней меньше, чем сумма квадратов отклонений от любой другой произвольной величины 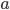 , т.е:
, т.е:
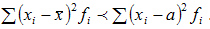
5. Если все варианты ряда уменьшить или увеличить на одно и то же число 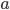 , то средняя уменьшится на это же число
, то средняя уменьшится на это же число 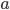 :
:
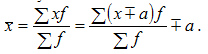
6.Если все варианты ряда уменьшить или увеличить в 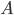 раз, то средняя также уменьшится или увеличится в
раз, то средняя также уменьшится или увеличится в 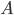 раз:
раз:
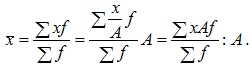
7.Если все частоты (веса) увеличить или уменьшить в 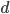 раз, то средняя арифметическая не изменится:
раз, то средняя арифметическая не изменится:
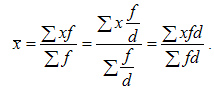
14. Средняя гармоническая — используется в тех случаях когда известны индивидуальные значения признака 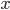 и произведение
и произведение 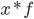 , а частоты
, а частоты 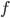 неизвестны.
неизвестны.
В примере ниже 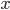 — урожайность известна,
— урожайность известна, 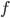 — площадь неизвестна (хотя её можно вычислить делением валового сбора зерновых на урожайность),
— площадь неизвестна (хотя её можно вычислить делением валового сбора зерновых на урожайность), 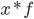 — валовый сбор зерна известен.
— валовый сбор зерна известен.
Среднегармоническую величину можно определить по следующей формуле:
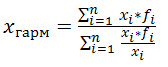
Формула средней гармонической:
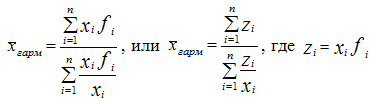
 2015-01-21
2015-01-21 5285
5285
