2015-02-24
5570
Как видно из выражений (4.9, 4.10, 4.11) кинематические параметры ведомого звена зависят от скорости ведущего. Для удобства анализа работы механизма скорости и ускорения ведомых звеньев удобно выражать в функции обобщенных координат ведущего звена, в качестве которых выбираются либо угол поворота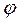 
, либо перемещение S ведущего звена.
Так как угол поворота к-го звена является функцией от угла ведущего звена, то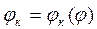 
откуда
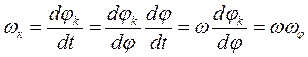(4.12)
Где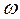 
- угловая скорость ведущего звена,
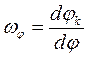-безразмерная угловая скорость к-го ведомого звена, которую называют аналогом угловой скорости.
Для углового ускорения, рассуждая аналогично, можно получить:
,
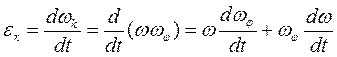Или
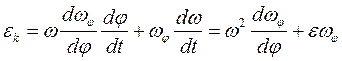
откуда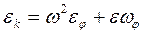 
(4.13)
Где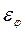 
- безразмерная величина – аналог углового ускорения ведомого звена.
Для линейных величин скоростей и ускорени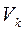й (
и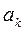 
) ведомого звена можно аналогично получить:
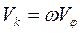(4.14)
и
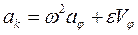(4.15)
Где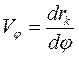 
- величина – аналог скорости к-го звена,
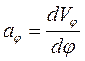- аналог ускорения.
При этом величины-аналоги скорости и ускорения имеют размерность (м).
Так как аналоги скоростей и ускорений зависят только от обобщенных координат и не зависят от времени кинематическое исследование механизма можно вести чисто геометрическим методом.
|
|
|
Для рассмотренного выше примера расчета КПМ аналогами скорости и ускорения ползуна, как следует из выражений (4.10 и 4.11), очевидно будут:
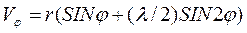(4.16)
и
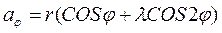(4.17)
Произвольное движение механизма, как было предложено Н.Е.Жуковским, может быть представлено в виде суммы перманентного или основного движении, при котором скорость ведущего звена постоянна (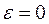
) и начального движения для которого (
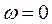). Тогда:
Для перманентного движения получим:
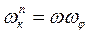
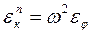(4.18)
.
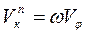
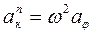Для начального движения:
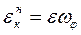(4.19)
.
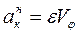Таким образом, истинное движение к-го звена механизма будет:
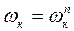
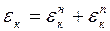(4.20)
.
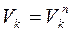
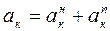Представление движения механизма состоящим из перманентного и начального позволяет определять положения, скорости и ускорения звеньев в функции обобщенных координат, а не в функции времени. Истинный закон изменения обобщенных координат от времени может быть определен только после динамического исследования механизма.
