Пусть событие 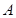 , о котором шла речь в формуле полной вероятности, уже произошло. То, что событие
, о котором шла речь в формуле полной вероятности, уже произошло. То, что событие 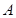 произошло, изменит вероятности гипотез
произошло, изменит вероятности гипотез 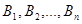 и условная вероятность гипотез
и условная вероятность гипотез 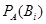 в предложении, что событие
в предложении, что событие 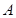 произошло, определится по формуле Бейеса:
произошло, определится по формуле Бейеса:
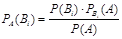 (3)
(3)
Замечание: иногда эту формулу называют формулой Байеса.
Значение формулы Бейеса состоит в том, что при наступлении события 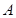 , т.е. по мере получения новой информации, мы можем проверять и корректировать выдвинутые до испытания гипотезы. Такой подход, называемый бейесовским, дает возможность корректировать управленческие решения в экономике, оценки неизвестных параметров распределения изучаемых признаков в статистическом анализе и т.п.
, т.е. по мере получения новой информации, мы можем проверять и корректировать выдвинутые до испытания гипотезы. Такой подход, называемый бейесовским, дает возможность корректировать управленческие решения в экономике, оценки неизвестных параметров распределения изучаемых признаков в статистическом анализе и т.п.
Задача 2. На сборку поступают детали из трех цехов в отношении 1:3:6. Количество бракованных деталей в продукции цехов соответственно равно 5%, 2%, 8%. Определить вероятность того, что:
а) наудачу взятая деталь окажется бракованной;
б) оказавшаяся бракованной деталь изготовлена во втором цехе.
Решение: Обозначим через 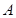 - событие, что взятая наудачу деталь окажется бракованной. Так как на сборку поступают детали из трех цехов, то эта деталь может быть изготовлена либо 1 цехом (гипотеза
- событие, что взятая наудачу деталь окажется бракованной. Так как на сборку поступают детали из трех цехов, то эта деталь может быть изготовлена либо 1 цехом (гипотеза 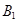 ), либо 2 (гипотеза
), либо 2 (гипотеза 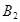 ), либо 3 (гипотеза
), либо 3 (гипотеза 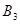 ). Следовательно, вероятность события
). Следовательно, вероятность события 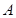 может быть найдена по формуле полной вероятности:
может быть найдена по формуле полной вероятности:
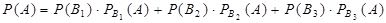
Вероятности гипотез 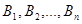 , определим по классической формуле
, определим по классической формуле 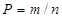 , если в качестве
, если в качестве 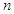 принять сумму всех частей, а в качестве
принять сумму всех частей, а в качестве 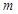 - соответствующее количество частей для данного цеха.
- соответствующее количество частей для данного цеха.
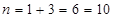 ,
, 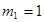 ,
, 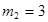 ,
, 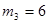
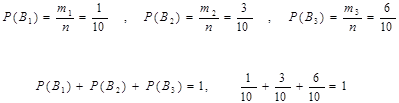
Находим условные вероятности:
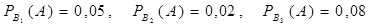 .
.
а) Вычисляем вероятность события 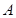 .
.
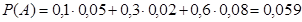
б) Используя формулу Бейеса, получим:
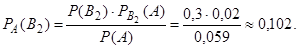
Если по формуле Бейеса подсчитать условные вероятности всех гипотез, то они в сумме должны равняться единице.
 2015-02-27
2015-02-27 2535
2535
