Система m линейных уравнений с n переменными имеет вид:
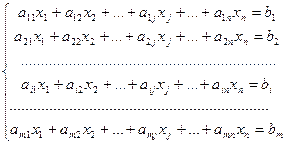 (1)
(1)
где 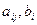
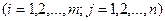 - произвольные числа, называемые соответственно коэффициентами при переменных и свободными членами уравнений.
- произвольные числа, называемые соответственно коэффициентами при переменных и свободными членами уравнений.
Решением системы называется такая совокупность n чисел, при подстановке которых каждое уравнение системы обращается в верное равенство.
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.
Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Пример:
1) 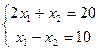 2)
2) 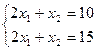 3)
3) 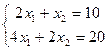
Две системы называются равносильными, или эквивалентными, если они имеют одно и то же множество решений.
Запишем систему (1) в матричной форме. Обозначим:
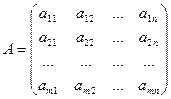 ;
; 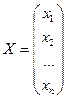 ;
; 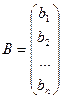 ,
,
где А – матрица коэффициентов при переменных, или матрица системы; Х – матрица-столбец переменных; В – матрица-столбец свободных членов.
Систему (1) можно записать в виде: АХ = В.
2. Система n линейных уравнений с n переменными. Метод обратной матрицы и формулы Крамера.
Пусть число уравнений системы (1) равно числу переменных, т.е. m=n. Тогда матрица системы является квадратной, а ее определитель 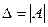 называется главным определителем системы.
называется главным определителем системы.
Умножая слева обе части матричного равенства на матрицу А-1, получим А-1(АХ)=А-1В. Так как А-1(АХ)=(А-1А)Х=ЕХ=Х, то решением системы методом обратной матрицы будет матрица столбец Х=А-1В.
Пусть дана система трех линейных алгебраическихуравнений с тремя неизвестными 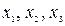 :
:
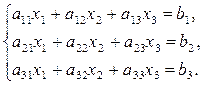 (2)
(2)
(коэффициенты aij и свободные члены bj для i = 1, 2, 3, j = 1, 2, 3 считаются заданными).
Тройка чисел 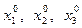 называется решением системы (2), если в результате подстановки этих чисел вместо
называется решением системы (2), если в результате подстановки этих чисел вместо 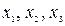 все три уравнения системы обращаются в тождества.
все три уравнения системы обращаются в тождества.
Систему (2) можно переписать в матричном виде:
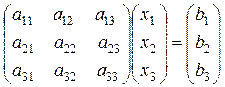 , или AX = B,
, или AX = B,
где A – это матрица коэффициентов при неизвестных, Х – столбец неизвестных, В – столбец свободных членов:
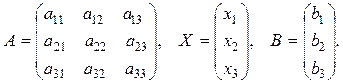
Составим определитель матрицы А и три вспомогательных определителя:
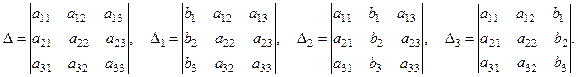 (3)
(3)
Вспомогательные определители Δ1, Δ2 и Δ3 получаются из Δ заменой элементов соответственно первого, второго и третьего столбцов столбцом свободных членов.
Если определитель 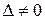 , то существует единственное решение системы (2) и оно выражается формулами:
, то существует единственное решение системы (2) и оно выражается формулами:
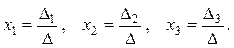 (4)
(4)
Теорема Крамера. Пусть 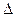 - главный определитель системы, а
- главный определитель системы, а 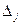 - определитель матрица, получаемой из матрицы А заменой j-го столбца столбцом свободных членов. Тогда, если
- определитель матрица, получаемой из матрицы А заменой j-го столбца столбцом свободных членов. Тогда, если 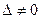 , то система имеет единственное решение, определяемое по формулам:
, то система имеет единственное решение, определяемое по формулам:
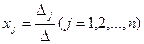 (5)
(5)
Формулы (5) называются формулами Крамера.
Пример: Решить систему уравнений 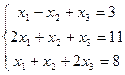 а)методом обратной матрицы; б) по формулам Крамера.
а)методом обратной матрицы; б) по формулам Крамера.
3. Метод Гаусса.
Метод Гаусса – метод последовательного исключения переменных – заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Преобразования Гаусса удобно проводить, осуществляя преобразования не с самими уравнениями, а с матрицей их коэффициентов. Рассмотрим матрицу
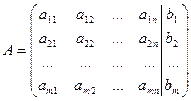 ,
,
называемую расширенной матрицей системы (1), потому что в нее кроме матрицы системы А, дополнительно включен столбец свободных членов.
Пример:
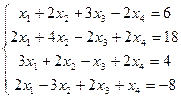
Расширенная матрица системы имеет вид:
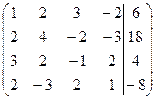
Шаг 1. Так как 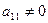 , то умножая первую строку на числа -2, -3, -2 и прибавляя полученные строки соответственно ко второй, третьей, четвертой строкам, исключим переменную х1 из всех строк, начиная со второй. Заметив что в новой матрице
, то умножая первую строку на числа -2, -3, -2 и прибавляя полученные строки соответственно ко второй, третьей, четвертой строкам, исключим переменную х1 из всех строк, начиная со второй. Заметив что в новой матрице 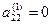 , поменяем местами вторую и третью строки:
, поменяем местами вторую и третью строки:

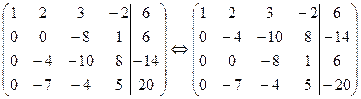
Шаг 2. Так как теперь 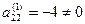 , то умножая вторую строку на -7/4 и прибавляя полученную строку к четвертой, исключим переменную х2 из всех строк, начиная с третьей:
, то умножая вторую строку на -7/4 и прибавляя полученную строку к четвертой, исключим переменную х2 из всех строк, начиная с третьей:
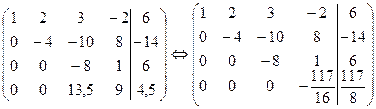
Шаг 3. Учитывая, что 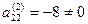 , умножаем третью строку на 13,5/8=27/16, и прибавляя полученную строку к четвертой, исключим из нее переменную х3. Получим систему уравнений
, умножаем третью строку на 13,5/8=27/16, и прибавляя полученную строку к четвертой, исключим из нее переменную х3. Получим систему уравнений
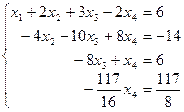
откуда найдем из четвертого уравнения х4 =-2; из третьего 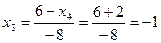 ; из второго
; из второго 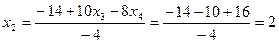 и из первого уравнения
и из первого уравнения 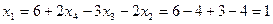 .
.
 2015-02-04
2015-02-04 5877
5877
