П.3. Уравнения прямой в пространстве

Параметрические уравнения прямой l в пространстве:

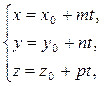(51)

где 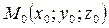– фиксированная точка прямой;

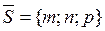– направляющий вектор прямой l, т.е. любой вектор, параллельный l;

t – числовой параметр.

Каждому значению параметра 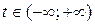соответствует единственная точка прямой l.

Канонические уравнения прямой:

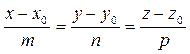. (52)

Уравнения прямой, проходящей через две данные точк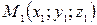и и :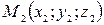

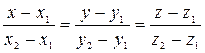. (53)

Углом 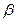между прямыми называют угол между их направляющими векторами 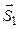={ m ₁; n ₁; p ₁} и 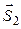={ m ₂; n ₂; p ₂}, или дополнительный к нему (обычно берется острый угол), то есть

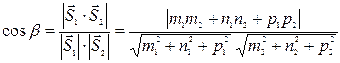. (54)

Углом между плоскостью и прямой l (в случае их пересечения) называется угол между прямой и её проекцией на плоскость. Синус угла 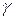между плоскостью 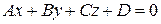и прямой 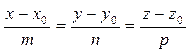определяется по формуле:

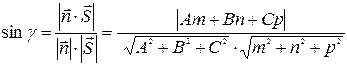. (55)