Закон распределения непрерывной случайной величины 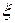 удобно задавать с помощью функции плотности вероятности
удобно задавать с помощью функции плотности вероятности 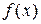 . Вероятность
. Вероятность 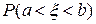 того, что значение, принятое случайной величиной
того, что значение, принятое случайной величиной 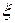 , попадет в интервал
, попадет в интервал 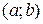 , определяется равенством:
, определяется равенством:
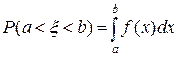 .
.
Функция распределения F(x) случайной величиной 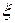 представима в виде
представима в виде
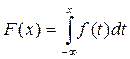
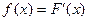
Математическим ожиданием или средним значением непрерывной случайной величины 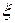 с плотностью распределения вероятности
с плотностью распределения вероятности 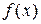 называется число:
называется число:
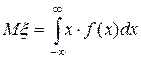 ,
,
если этот интеграл сходится абсолютно. В противном случае математическое ожидание случайной величины 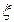 не существует.
не существует.
Дисперсия непрерывной случайной величины определяется также, как и для дискретной. Для непосредственного вычисления дисперсии используют формулы:
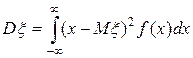 или
или 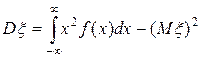 .
.
Задача 4. Плотность распределения вероятностей непрерывной случайной величины имеет вид:
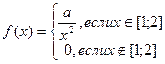 . Найти а,
. Найти а, 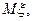
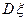
 2015-02-04
2015-02-04 703
703







