Непрерывная случайная величина имеет нормальное или гауссовское распределение с параметрами 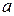 и
и 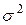 , где
, где 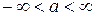 и
и 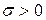 (пишут
(пишут 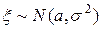 ), если функция плотности случайной величины имеет вид:
), если функция плотности случайной величины имеет вид:
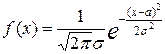 ,
,
для любого 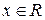 .
.
При 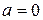 и
и 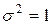 , т.е.
, т.е. 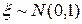 , нормальный закон распределения называется стандартным или нормированным.
, нормальный закон распределения называется стандартным или нормированным.
Если случайная величина 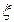 имеет нормальное распределение с параметрами
имеет нормальное распределение с параметрами 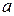 и
и 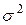 , то
, то
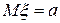 и
и 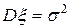 .
.
Найти вероятность попадания случайной величины 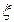 , распределенной по нормальному закону с параметрами
, распределенной по нормальному закону с параметрами 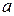 и
и 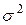 , в интервал
, в интервал 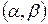 можно по формуле:
можно по формуле:
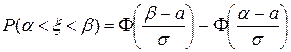 , (11)
, (11)
где 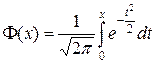 – функции Лапласа, значения которой определяются по таблице. При использовании таблицы необходимо учитывать, что функция
– функции Лапласа, значения которой определяются по таблице. При использовании таблицы необходимо учитывать, что функция 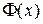 является нечетной и при
является нечетной и при 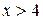 значения
значения 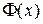 считаются равными 0,5.
считаются равными 0,5.
Задача 5. Случайная величина 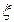 распределена по нормальному закону с математическим ожиданием
распределена по нормальному закону с математическим ожиданием 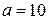 и дисперсией
и дисперсией 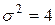 . Найти вероятность того, что в результате испытания
. Найти вероятность того, что в результате испытания 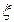 примет значение, заключенное в интервале
примет значение, заключенное в интервале 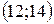 .
.
Решение.
Так как случайная величина 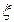 имеет нормальное распределение, то вероятность ее попадания в интервал можно найти по формуле (11). Учитывая, что по условию имеем:
имеет нормальное распределение, то вероятность ее попадания в интервал можно найти по формуле (11). Учитывая, что по условию имеем: 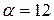 ,
, 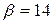 ,
, 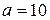 ,
, 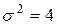 , то получим:
, то получим:
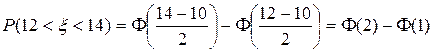 .
.
По таблице значений функции Лапласа 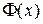 находим: F(2)=0,4772, F(1)=0,3413. Значит, получаем:
находим: F(2)=0,4772, F(1)=0,3413. Значит, получаем: 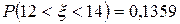 .
.
Ответ: 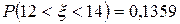
 2015-02-04
2015-02-04 551
551








