2015-02-04
4323
Критерием согласия называется критерий проверки гипотезы о предполагаемом законе распределения.
Критерий согласия Пирсона (критерий проверки гипотезы о нормальном распределении генеральной совокупности):
1) По выборке объема n построить статистический ряд:
| xi | x 1 | x 2 | … | xl |
| mi | m 1 | m 2 | … | ml |
2) Вычислить по таблице оценку математического ожидания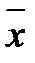 
и выборочное среднее квадратическое отклонение σ в .
3) В предположении нормального распределения генеральной совокупности вычислить теоретические частоты m 1 теор,…, ml теор по формуле:
m 1 теор= n · pi,
где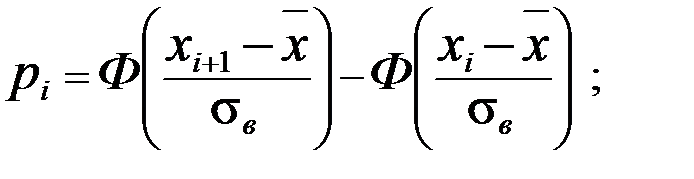 
Ф (x) – интегральная функция распределения Лапласа - табл. П 2.2(см. приложение 2).
4) Вычислить число χ 2набл по формуле:
χ 2набл =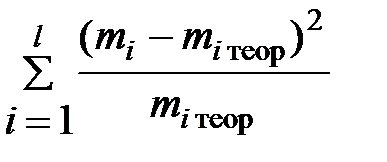 
или χ 2набл = 
.
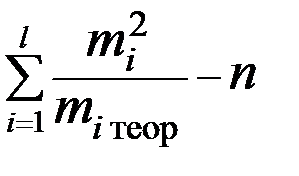5) По табл. П 2.5 (приложение 2) найти число χ 2крит, учитывая заданный уровень значимости α и число степеней свободы k = l – 3.
6) Сравнить числа χ 2набл и χ 2крит:
· если χ 2набл < χ 2крит, то нет основания отвергать гипотезу о нормальном распределении генеральной совокупности.
· если χ 2набл > χ 2крит , то гипотезу о нормальном распределении генеральной совокупности следует отвергнуть.
Замечание 1. Объем выборки n должен быть достаточно велик (больше 100). Число l обычно выбирают в диапазоне от 7 до 15. Поэтому при составлении интервального статистического ряда не используют интервалы, содержащие малое число значений объединяя их в один и суммируя соответствующее число значений.
Замечание 2. В случае χ 2набл < χ 2крит , для избежания ошибки первого рода следует повторить опыт, увеличив число n.
Замечание 3. При использовании критерия Пирсона с целью систематизации записи рекомендуется записывать все промежуточные вычисления в виде следующей таблицы:
| № | xi | mi | mi 2 | mi теор |  |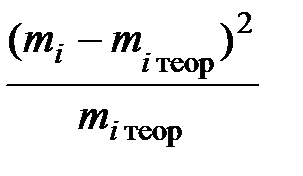
| … | |||||
| l | |||||
| ∑ | n | n | χ 2набл |
