Правило проверки наличия связи между качественными признаками

Для обоснованного суждения о наличии связи между качественными признаками А и В генеральной совокупности Х следует проверить, значим ли выборочный коэффициент их ранговой корреляции.

1) Пусть при уровне значимости α нулевая гипотеза H ₀ : между признаками А и В нет значимой связи.

· По табл. П 2.6 критических точек распределения Стьюдента (см. приложение 2) по уровню значимости α и числу степеней свободы k = n – 2 найти число t _крит ;

· Найти число ,

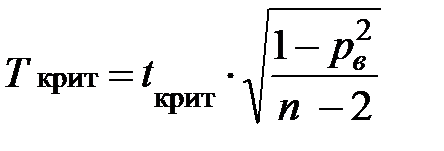где n – объем выборки;

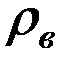– выборочный коэффициент ранговой корреляции Спирмена;

· Сравнить числа , :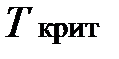

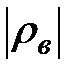если 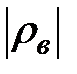< 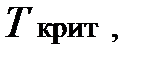то нет основания отвергать гипотезу H ₀ , т.е. ранговая корреляция между признаками не значима;

если 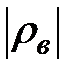> 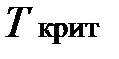то нулевая гипотеза H ₀ отвергается, т.е. между качественными признаками существует значимая корреляционная связь.

2) Пусть при уровне значимости α нулевая гипотеза H ₀: между признаками А и В генеральной совокупности нет значимой связи.

· По табл. П 2.2 функции Лапласа (см. приложение 2) по уровню значимости α из равенства 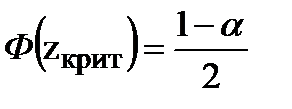найти число ;

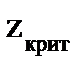· Найти число ,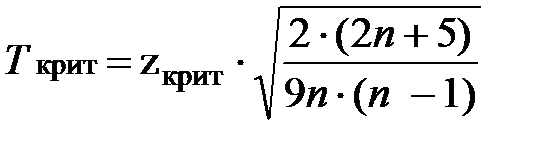

где 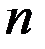– объем выборки;

· Сравнить числа , :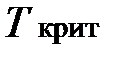

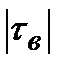если 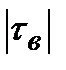< 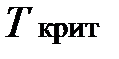, то нет основания отвергать гипотезу H ₀ , т.е. ранговая корреляция между признаками не значима;

если 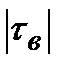> 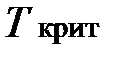, то нулевая гипотеза H ₀ отвергается, т.е. между качественными признаками существует значимая корреляционная связь.