Задача 11.1. Найти выборочный коэффициент корреляции и уравнение линейной регрессии Y на X по данным пяти наблюдений:
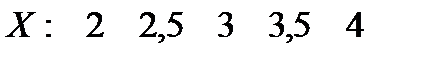
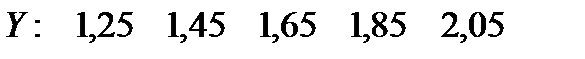
Решение. Используем формулы:
1) Выборочный коэффициент корреляции:
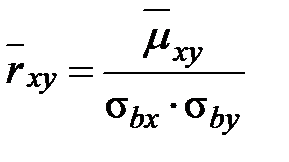 =
= 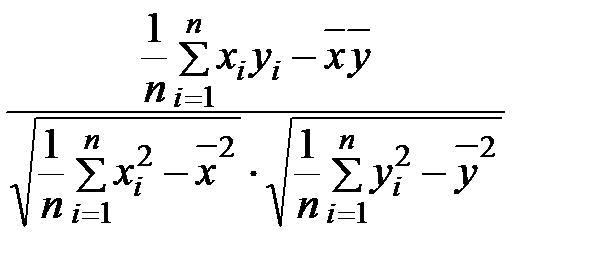 ;
;
2) линейное уравнение регрессии Y на X:
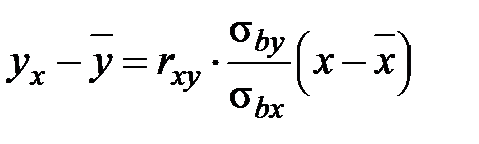 ,
,
где 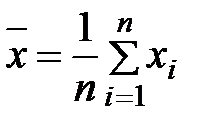 ,
, 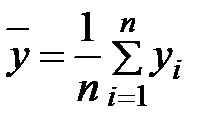
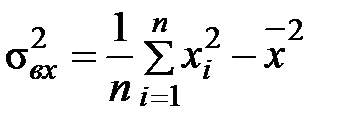 ,
, 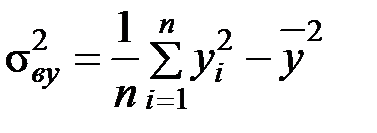 ,
, 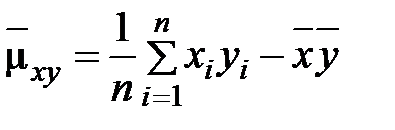 .
.
Проведем необходимые вычисления, для чего составим расчетную таблицу:
| № | 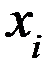 | 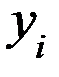 | 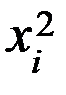 | 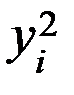 | 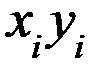 |
| 1,25 | 1,5625 | 2,5 | |||
| 2,5 | 1,45 | 6,25 | 2,1025 | 3,625 | |
| 1,65 | 2,7225 | 4,95 | |||
| 3,5 | 1,85 | 12,25 | 3,4225 | 6,475 | |
| 2,05 | 4,2025 | 8,2 | |||
| ∑ | 8,25 | 47,5 | 14,0125 | 25,75 |
Тогда получаем:
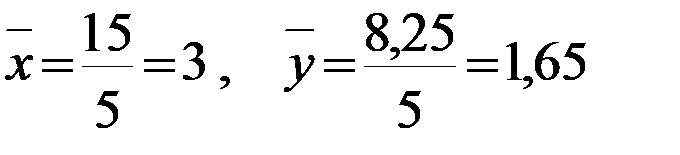 ,
,
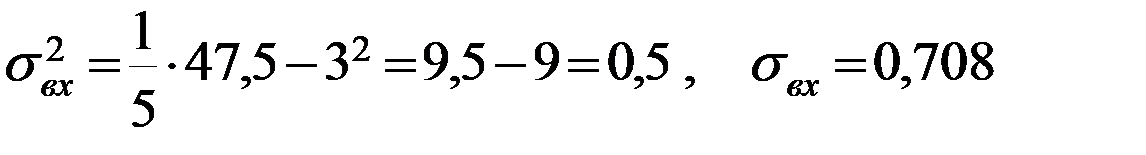
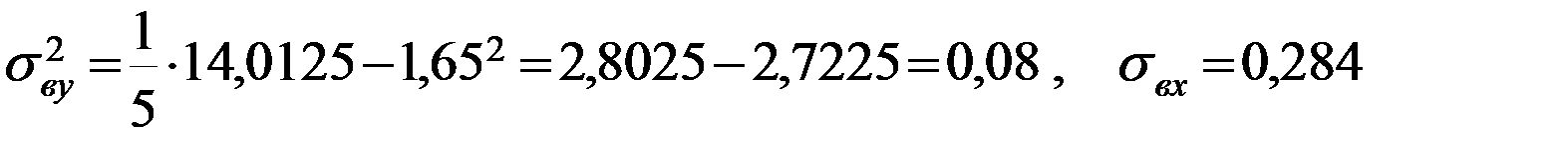 ,
,
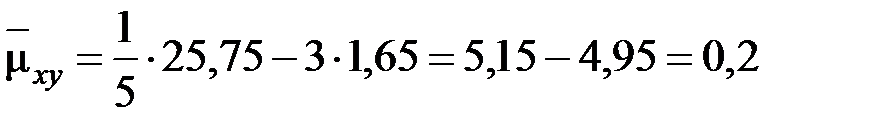 ,
,
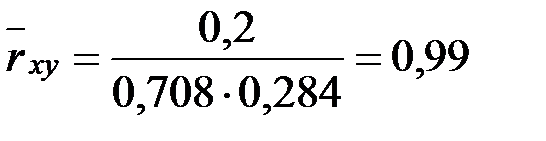 .
.
Запишем уравнение линейной регрессии Y на X:
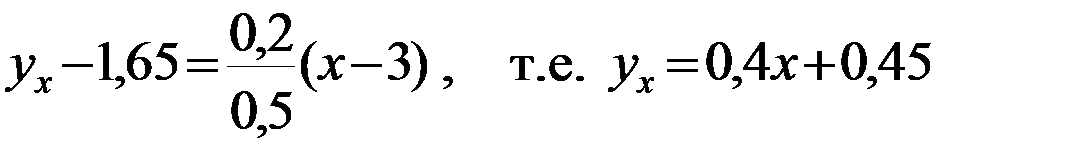 .
.
Ответ: 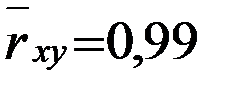 ,
, 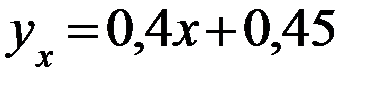 .
.
Задача 11.2. Найти выборочный коэффициент корреляции и выборочные уравнения линейных регрессий Y на X и X на Y по данным выборки X и Y, сведенным в корреляционную таблицу:
| Y X | 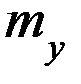 | ||||||||
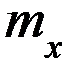 | 8 | 6 |
Решение.
1) Найдем оценки математических ожиданий X и Y:
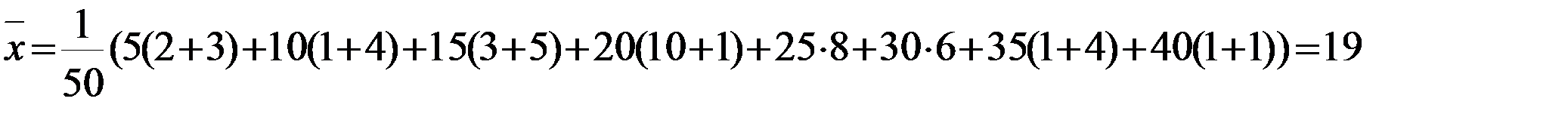 ;
;
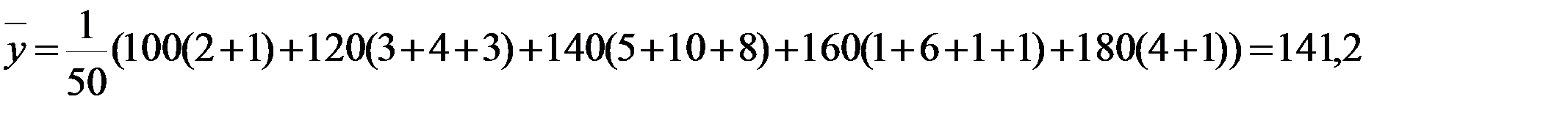
2) Найдем выборочные дисперсии:
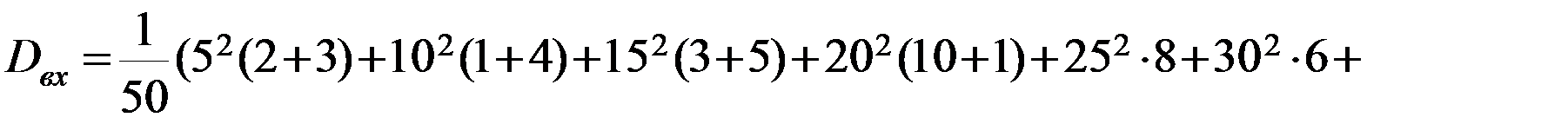
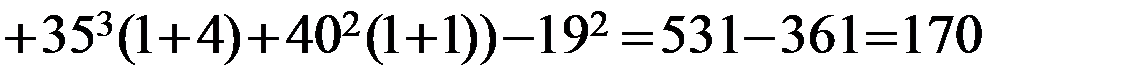 ,
,
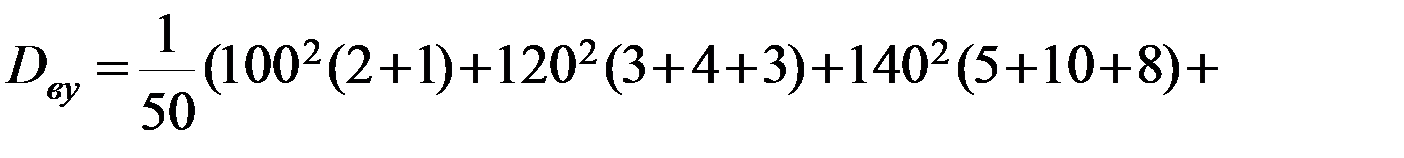
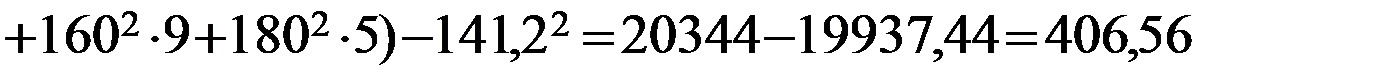 .
.
3) Найдем выборочные средние квадратические отклонения:
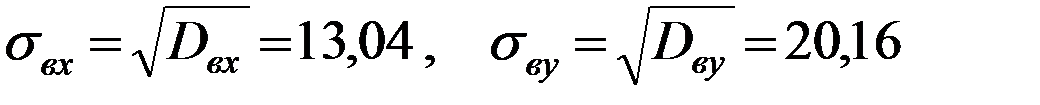 .
.
4) Найдем выборочный корреляционный момент:
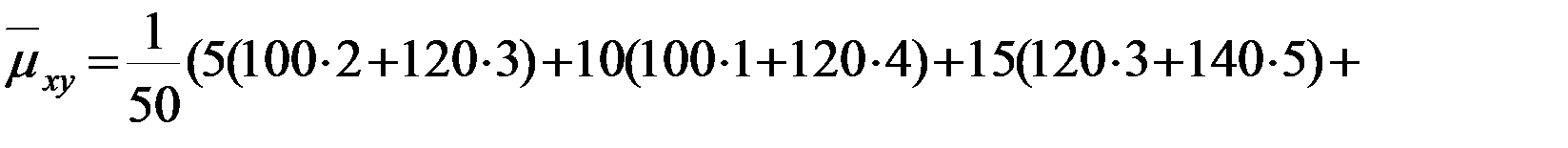
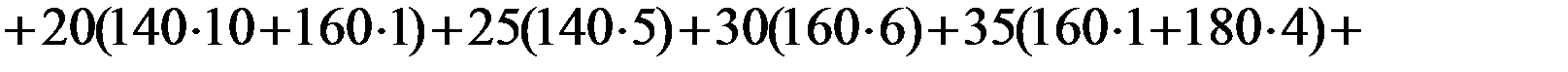
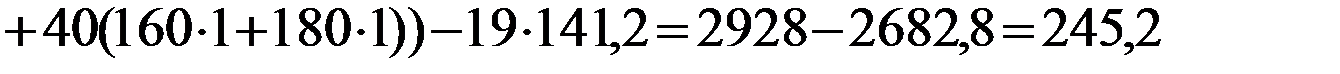 .
.
5) Найдем выборочный коэффициент корреляции:
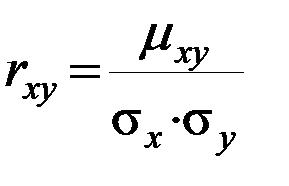 =
= 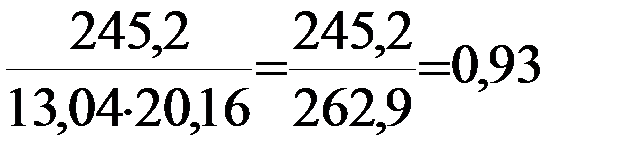 .
.
6) Напишем выборочное уравнение линейной регрессии Y на X:
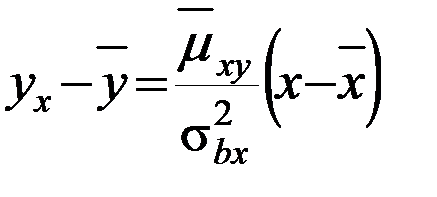
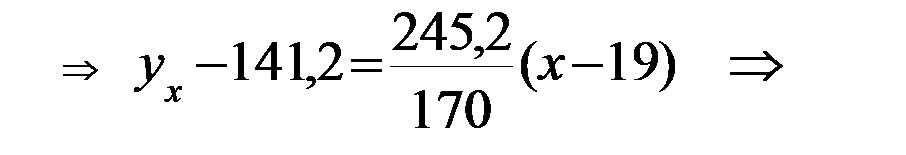
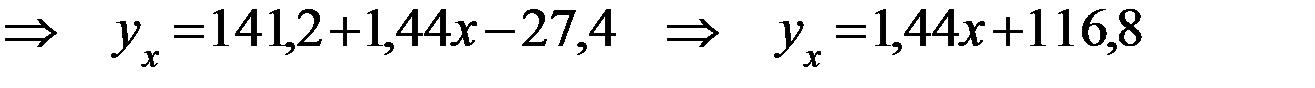
7) Напишем выборочное уравнение линейной регрессии X на Y:
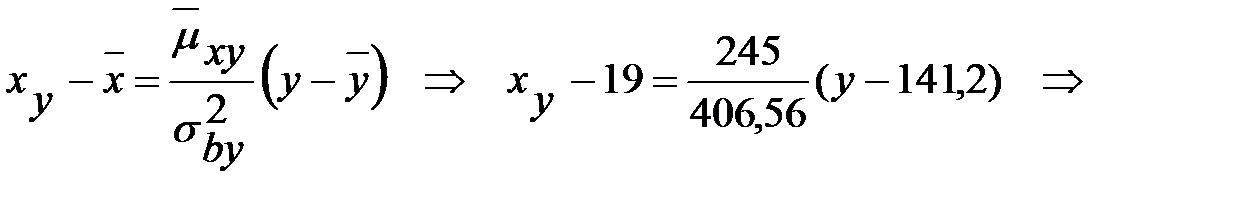
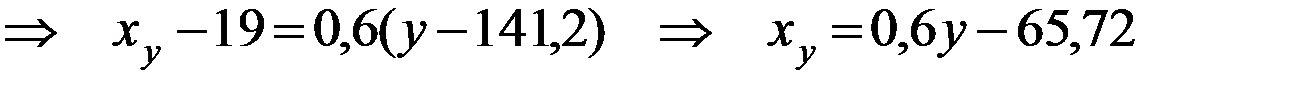
Ответ: 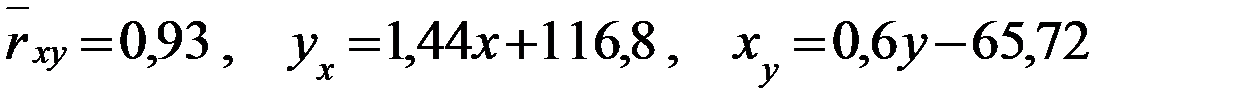 .
.
Задача 11.3. Знания 10 студентов проверены по двум тестам А и В. Оценки по стобальной системе оказались следующими:
По А: 92 96 90 50 75 83 65 70 62 55
По В: 94 98 84 52 70 87 62 74 59 50.
Найти выборочный коэффициент ранговой корреляции: а) Спирмена; б) Кендалла и оценить их значимость при уровне значимости α=0,1.
Решение. 1) Присвоим ранги ai оценкам xi по тесту А, расположив эти оценки в порядке убывания:
| ai | ||||||||||
| xi |
2) Присвоим ранги bi оценкам yi по тесту В, расположив их в порядке убывания:
| bi | ||||||||||
| yi |
3) Рангу a 1=1 оценки 96 по тесту А соответствует ранг b 1 оценки 98 (первого студента) по тесту В
Рангу a 2=2 оценки 92 по тесту А соответствует ранг b 2=2 оценки 94 по тесту В.
Рангу a 3=3 оценки 90 по тесту А соответствует ранг 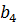 =4 оценки 84.
=4 оценки 84.
Аналогично получаем:
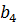 = 3,
= 3, 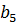 = 6,
= 6, 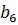 =5,
=5, 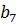 =7,
=7, 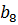 =8,
=8, 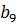 =10,
=10, 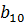 =9.
=9.
4) Выпишем последовательности рангов 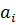 и
и 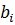 :
:
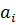 | ||||||||||
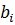 |
и получим разности рангов:
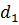 =
= 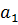
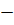
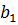 = 0;
= 0; 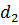 =
= 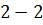 =0;
=0; 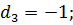
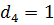 ;
; 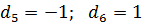 ;
; 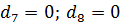 ;
; 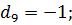
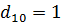 .
.
5) Вычислим выборочный коэффициент ранговой корреляции Спирмена:
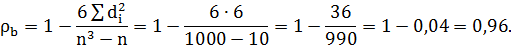
6) Вычислим выборочный коэффициент ранговой корреляции Кендалла:
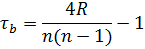
где 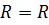 1 + R 2 +…+ Rn -1 = 9 + 8 + 6 + 6 + 4 + 4 + 3 + 2 + 0 = 42.
1 + R 2 +…+ Rn -1 = 9 + 8 + 6 + 6 + 4 + 4 + 3 + 2 + 0 = 42.
Тогда получаем:
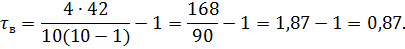
7) При уровне значимости 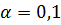 находим число
находим число
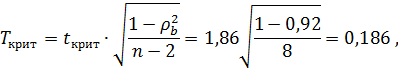
Сравниваем числа T крит и 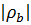 : так как 0,96 > 0,186, то
: так как 0,96 > 0,186, то 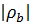 > T крит и ранговая корреляция между признаками является значимой.
> T крит и ранговая корреляция между признаками является значимой.
8) При уровне значимости α = 0,1 находим:
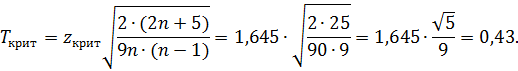
Сравним числа 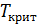 и
и 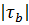 :
:
так как 0,87 > 0,43, то 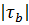 >
> 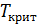
Значит корреляционная связь между сравниваемыми оценками значимая.
Ответ: 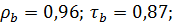 гипотеза о наличии корреляционной связи между оценками принимается.
гипотеза о наличии корреляционной связи между оценками принимается.
Задачи
11.1. Найдите выборочный коэффициент корреляции и выборочное линейное уравнение Y на X по данным семи наблюдений:
| xi | 4,0 | 4,25 | 4,5 | 4,75 | 5,0 | 5,25 | 5,5 |
| yi | 1,25 | 1,35 | 1,50 | 1,65 | 1,80 | 2,05 | 2,30 |
11.2. Найдите выборочный коэффициент корреляции и выборочное линейное уравнение Y на X по данным пяти наблюдений:
| xi | 1,25 | 2,05 | 3,1 | 3,95 | 5,0 |
| yi | 4,2 | 2,5 | 3,5 | 1,0 | 2,1 |
11.3. Даны результаты 50-ти наблюдений, собранные в корреляционную таблицу:
| Y X | my | |||||||
| mi |
Найти выборочный коэффициент корреляции и выборочные линейные уравнения регрессий Y на X и X на Y, проверив гипотезу значимости выборочного коэффициента корреляции при уровне значимости 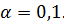
11.4. По данным 50-ти наблюдений, собранным в корреляционную таблицу:
| Y X | my | |||||||
| mi |
Найти выборочный коэффициент корреляции и выборочные линейные уравнения регрессий Y на X и X на Y, проверив гипотезу значимости выборочного коэффициента корреляции при уровне значимости 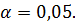
11.5. В результате 79 опытов получена корреляционная таблица:
| Y X | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | my |
| 0,5 | ||||||
| 0,6 | ||||||
| 0,7 | ||||||
| 0,8 | ||||||
| mi |
Определить выборочный коэффициент корреляции, проверить гипотезу значимости коэффициента корреляции при уровне значимости 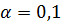 , написать выборочные уравнения регрессий Y на X и X на Y.
, написать выборочные уравнения регрессий Y на X и X на Y.
11.6. В результате 60 опытов получена корреляционная таблица величин X и Y:
| Y X | 7,0 | 7,5 | 8,0 | 8,5 | 9,0 | 9,5 | my |
| mi |
Определить выборочный коэффициент корреляции, проверить гипотезу значимости коэффициента корреляции при уровне значимости 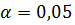 , написать выборочные уравнения регрессий Y на X и X на Y.
, написать выборочные уравнения регрессий Y на X и X на Y.
11.7. Знания 10 студентов оценены двумя преподавателями по стобальной системе и выставлены следующие оценки:
Найти выборочные коэффициенты ранговой корреляции Спирмена и Кендалла и проверить их значимость при уровне значимости 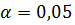 .
.
11.8. Два контролера расположили 10 деталей в порядке ухудшения их качества. В результате получены две последовательности рангов:
Найти выборочные коэффициенты ранговой корреляции Спирмена и Кендалла и проверить их значимость при уровне значимости 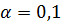 .
.
11.9. Три арбитра A, B и C оценили мастерство 10 спортсменов. В итоге были получены три последовательности рангов:
| A: | 10; | |||||||||
| B: | 4; | |||||||||
| C: | 8. |
Определите пару арбитров, оценки которых наиболее согласуются, используя:
а) выборочный коэффициент ранговой корреляции Спирмена;
б) выборочный коэффициент ранговой корреляции Кендалла.
Ответы
11.1. 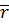 xy = 0,99;
xy = 0,99; 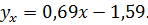
11.2. 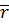 xy =
xy = 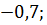
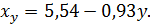
11.3. 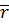 xy = 0,84;
xy = 0,84; 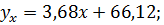
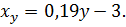
11.4. 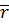 xy =
xy = 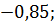
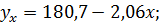
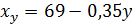 .
.
11.5. 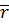 xy =
xy = 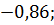
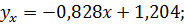
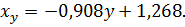
11.6. 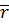 xy = 0,71;
xy = 0,71; 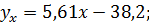
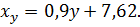
11.7. 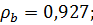
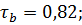 гипотеза о наличии корреляционной связи между оценками принимается.
гипотеза о наличии корреляционной связи между оценками принимается.
11.8. 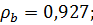
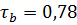 ; гипотеза о наличии корреляционной связи между наблюдаемыми величинами принимается.
; гипотеза о наличии корреляционной связи между наблюдаемыми величинами принимается.
11.9. a) 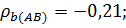
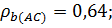
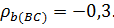
Наиболее согласуются оценки арбитров A и C;
б) 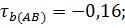
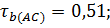
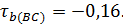
Наиболее согласуются оценки арбитров A и C.
Приложение 1
Контрольные работы и контрольные вопросы по теории
 2015-02-04
2015-02-04 25422
25422
