Идентификация нелинейных функций априорно известного вида

Если имеется априорная информацияо типе нелинейности, то параметры «истинных» нелинейных функций могут быть идентифицированы. В таких случаях можно использовать один из следующих приемов:

а) произвести замену переменных в исходном аналитическом выражении, затем, выполнив линеаризацию, получить линейную модель объекта. Рассмотрим процесс, описываемый выражением

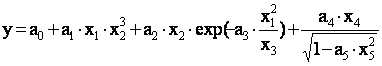(19.1)

Для идентификации этого процесса введем сначала следующие новые переменные:

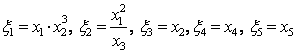(19.2)

В итоге получим:

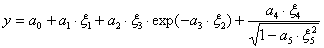. (19.3)

Линеаризуем теперь уравнение (19.3) в предположении, что приращения его переменных малы:

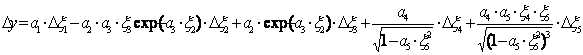(19.4)

Вводя обозначения

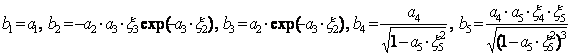(19.5)

получим

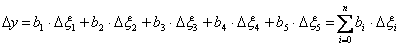. (19.6)

Очевидно, b₁, b₂,…,b₅ могут быть идентифицированы методом линейной регрессии. Замечая, что 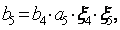можно определить а₅, поскольку 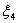и 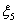доступны для измерения. Подставляя выражение для а₅ в формулу (19.5) для 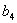, получаем 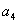. Член 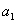непосредственно определяется величиной 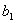согласно (19.5). Члены 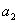, 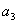можно найти из выражений (19.5) для 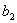, 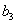следующим образом. Значение 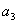находим из выражения 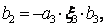где переменная 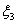доступна для измерения. Наконец, 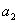определяется подстановкой 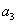в выражение (19.5) для .

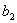По аналогии с описанной выше методикой идентификации процесса (19.1) может быть идентифицировано много других видов нелинейных зависимостей;

б) экспоненциальные зависимости вида 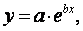могут быть идентифицированы, если преобразовать их путем логарифмирования к соотношению вида: 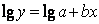. Обозначая 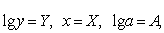получим 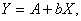где А и В легко вычисляются методом минимума среднеквадратичной ошибки.

Аналогично в процессах вида 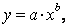можно использовать логарифмирование, получая выражение 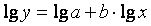, из которого а и в вычисляются так же, как и в предыдущем случае.

Однако, в некоторых случаях последний метод непригоден или для его применения необходима некоторая дополнительная информация. Например, этот метод непригоден для системы

,

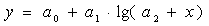в которой требуется идентифицировать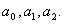

Используя метод малых возмущений, получим 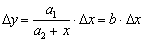. Здесь коэффициент 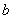может быть идентифицирован с помощью среднеквадратичного критерия 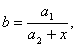однако это не дает решения для 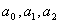. Можно, конечно, использовать вторые и высшие частные производные (или возмущения второго и последующих порядков), но на практике это обычно не имеет смысла, поскольку здесь значимость производных мала, особенно если измерения зашумлены.