Выше мы отмечали экономический смысл определенного интеграла, выражающего объем произведенной продукции при известной функции производительности труда.
Рассмотрим другие примеры использования интеграла в экономике.
Если в функции Кобба-Дуглоса считать, что затраты труда если линейная зависимость от времени, а затраты капитала неизменны, то она примет вид 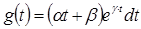 .
.
Тогда объем выпускаемой продукции за 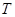 лет составит:
лет составит:
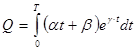 (22)
(22)
Пример. Найти объем продукции, произведений за 4 года, если функция Кобба-Дугласа имеет вид 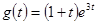 .
.
По формуле (22) объем 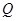 произведенной продукции равен
произведенной продукции равен
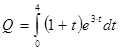 .
.
Используем метод интегрирования по частям. Пусть 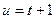 ,
, 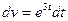 . Тогда
. Тогда 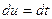 ,
, 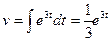 .
.
Следовательно,
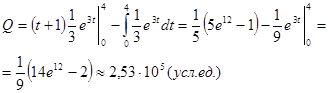
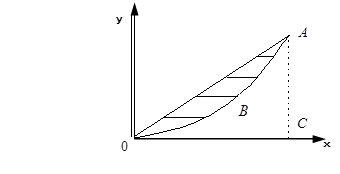
Исследуя кривую Лоренца – зависимость процента доходов от процента, имеющего их населения (кривую 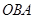 , см.рис.). Мы можем оценить степень неравенства в распределении доходов населения. При равномерном распределении доходов кривая Лоренца выражается в прямую – биссектрису
, см.рис.). Мы можем оценить степень неравенства в распределении доходов населения. При равномерном распределении доходов кривая Лоренца выражается в прямую – биссектрису 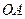 , поэтому площадь фигуры
, поэтому площадь фигуры 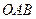 между биссектрисой
между биссектрисой 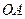 и кривой Лоренца, отнесенная к площади треугольника
и кривой Лоренца, отнесенная к площади треугольника 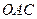 (коэффициент Джини), характеризует степень неравенства в распределении доходов населения.
(коэффициент Джини), характеризует степень неравенства в распределении доходов населения.
 |
Пример. По данным исследований в расположении доходов в одной из стран кривая Лоренца  может быть описана уравнением
может быть описана уравнением 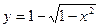 , где
, где 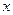 - доля населения,
- доля населения, 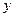 - доля доходов населения. Вычислить коэффициент Джини.
- доля доходов населения. Вычислить коэффициент Джини.
Коэффициент Джини (см. рис.)
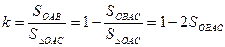 ,
,
так как
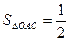 .
. 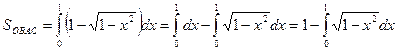 .
.
Поэтому
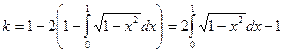 .
.
С помощью замены, например, 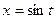 можно вычислить
можно вычислить 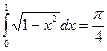 . Итак, коэффициент Джини
. Итак, коэффициент Джини 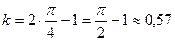 .
.
Достаточно высокое значение 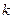 показывает существенно неравномерное распределение доходов среди населения в рассматриваемой стране.
показывает существенно неравномерное распределение доходов среди населения в рассматриваемой стране.
Определение начальной суммы по ее конечной величине, полученной через время 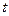 (лет) при годовом проценте (процентной ставке)
(лет) при годовом проценте (процентной ставке) 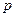 , называется дисконтированием. Задачи такого рода встречаются при определении экономической эффективности капитальных вложений.
, называется дисконтированием. Задачи такого рода встречаются при определении экономической эффективности капитальных вложений.
Пусть 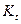 - конечная сумма, полученная за
- конечная сумма, полученная за 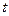 лет,
лет, 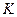 - дисконтируемая (начальная) сумма, которую в финансовом анализе называют также современной суммой. Если проценты простые, то
- дисконтируемая (начальная) сумма, которую в финансовом анализе называют также современной суммой. Если проценты простые, то 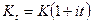 , где
, где 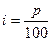 - удельная процентная ставка. Тогда
- удельная процентная ставка. Тогда 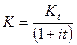 . В случае сложных процентов
. В случае сложных процентов 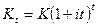 и потому
и потому 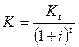 .
.
Пусть поступающий ежегодно доход изменяется во времени и описывается функцией 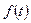 и при удельной норме процента, равной
и при удельной норме процента, равной 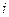 , процент начисляется непрерывно. Можно показать, что в этом случае дисконтированный доход
, процент начисляется непрерывно. Можно показать, что в этом случае дисконтированный доход 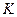 за время
за время 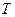 вычисляется по формуле:
вычисляется по формуле:
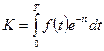 . (23)
. (23)
Пример. Определить дисконтированный доход за три года при процентной ставке 8%, если первоначальные (базовые) капиталовложения составили 10 млрд. руб.
Очевидно, что капиталовложения задаются функцией 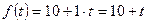 . Тогда по формуле (23) дисконтированная сумма капиталовложений
. Тогда по формуле (23) дисконтированная сумма капиталовложений 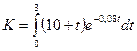 .
.
Используя метод интегрирования по частям, получим 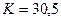 млрд. руб. Это означает, что для получения одинаковой наращенной суммы через три года ежегодные капиталовложения от 10 до 13 млрд. руб. равновесны одновременным первоначальным вложениям 30, 5 млрд. руб. при той же, начисляемой непрерывно, процентной ставке.
млрд. руб. Это означает, что для получения одинаковой наращенной суммы через три года ежегодные капиталовложения от 10 до 13 млрд. руб. равновесны одновременным первоначальным вложениям 30, 5 млрд. руб. при той же, начисляемой непрерывно, процентной ставке.
Пусть известна функция 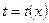 , описывающая изменение затрат времени
, описывающая изменение затрат времени 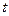 на изготовление изделия в зависимости от степени освоения производства, где
на изготовление изделия в зависимости от степени освоения производства, где 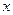 - порядковый номер изделия в партии. Тогда среднее время
- порядковый номер изделия в партии. Тогда среднее время 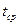 , затраченное на изготовление одного изделия в период освоения от
, затраченное на изготовление одного изделия в период освоения от 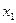 до
до 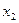 изделий, вычисляется по теореме о среднем:
изделий, вычисляется по теореме о среднем:
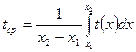 . (24)
. (24)
Что касается функции изменения затрат времени на изготовление изделий 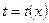 , то часто она имеет вид
, то часто она имеет вид
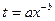 , (25)
, (25)
где 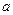 — затраты времени на первое изделие,
— затраты времени на первое изделие, 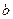 — показатель производственного процесса.
— показатель производственного процесса.
Пример. Найти среднее время, затраченное на освоение одного изделия в период освоения от 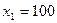 до
до 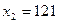 изделий, полагая в формуле (24)
изделий, полагая в формуле (24) 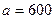 (мин.),
(мин.), 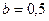 .
.
Получаем 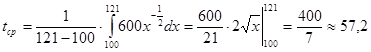 (мин.).
(мин.).
 2015-02-04
2015-02-04 3810
3810








