Будем рассматривать общий случай: векторную функцию векторного аргумента: 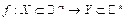 или
или 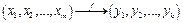 .
.
Существует два определения предела функции:
-по Гейне (на языке последовательностей);
-по Коши (на языке «ε-δ»-окрестностей).
Определение предела функции по Гейне:
Пусть 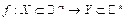 и
и 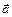 - предельная точка множества
- предельная точка множества 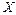 . Вектор
. Вектор 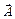 называется пределом функции
называется пределом функции 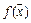 при
при 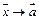 , если для любой последовательности
, если для любой последовательности 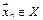 ,
, 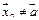 ,
, 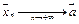 соответствующая последовательность значений функции
соответствующая последовательность значений функции 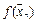 всякий раз сходится к
всякий раз сходится к 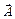 .
.
Для предела используют обозначение: 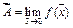 .
.
Определение сохраняет смысл для числовой функции, если 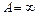 , и для числовой функции числового аргумента, когда
, и для числовой функции числового аргумента, когда 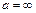 .
.
Определив предел функции через предел последовательности, мы можем использовать все теоремы, касающиеся предела последовательности.
Пример 1. Покажем, что 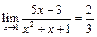 . Для любой последовательности
. Для любой последовательности 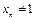 ,
, 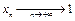 по теореме об арифметических свойствах предела последовательности имеем:
по теореме об арифметических свойствах предела последовательности имеем:
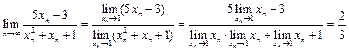
Определением предела функции по Гейне очень удобно пользоваться при доказательстве отсутствия предела функции.
Чтобы доказать, что 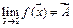 , достаточно указать хотя бы одну последовательность
, достаточно указать хотя бы одну последовательность 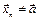 ,
, 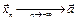 и такую, что
и такую, что 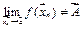 .
. 

Пример 2. Докажем, что 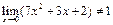 . Пусть
. Пусть 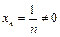 ,
, 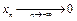 . Тогда
. Тогда 

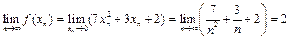 .
.
Если же потребуется доказать, что 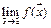 не существует, то необходимо выбрать две различные последовательности
не существует, то необходимо выбрать две различные последовательности 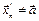 ,
, 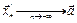 ,
, 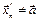 ,
, 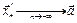 и такие, что
и такие, что 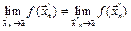 .
.
Пример 3.Покажем, что не существует 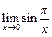 .
.
Выберем 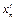 и
и 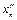 из условий:
из условий:
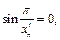
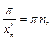
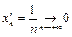 ,
,
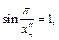
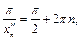
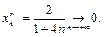
При этом 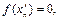
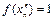 .
. 
Пример 4. Покажем, что функция Дирихле 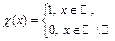 не имеет предела ни в одной точке
не имеет предела ни в одной точке 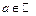 .
.
Пусть 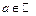 - произвольно, а
- произвольно, а 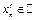 ,
, 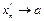 , тогда
, тогда 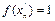 ,
, 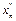 -последовательность иррациональных чисел,
-последовательность иррациональных чисел, 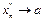 , тогда
, тогда 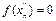 . Таким образом,
. Таким образом, 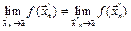 .
.
 2015-02-14
2015-02-14 861
861







