Симметричный и примитивный потоки

Симметричным потоком называется поток с простым последействием, параметр которого λ _S (t) в любой момент времени t зависит только от числа i обслуживаемых в этот момент заявок и не зависит от других характеристик, определяющих состояние S (t) системы. При этом зависимость параметра от числа обслуживаемых заявок может быть подчинена любому закону. Поэтому в любом состоянии S (t) с i обслуживаемыми заявками параметр симметричного потока один и тот же, он зависит только от i, т.е. λ _S (t) = λ _i.

Примитивным называется такой симметричный поток, параметр которого λ _i прямо пропорционален числу свободных в данный момент источников заявок.

λ _i = (n – i)a, (2.16)

где n – число источников заявок; i – число занятых источников; a – параметр потока источника в свободном состоянии (при этом имеет место естественное предположение – занятый источник не может производить заявки). В модели примитивного потока параметр источника a в свободном состоянии является постоянной величиной, а параметр примитивного источника λ _i убывает с увеличением числа занятых источников i. Математическое ожидание параметра примитивного λ определяется по формуле

,

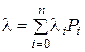где Р_i – вероятность того, что в системе занято i источников. Заметим, что обслуживающей примитивный поток системе не требуется более n обслуживающий устройств, т.е. занятый источник не может производить заявки.

Можно показать, что функция распределения вероятности длительности свободного состояния источника (промежуток времени между моментом окончания одного занятия и моментом поступления новой заявки)

.

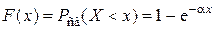Таким образом, промежуток времени между моментами окончания одного занятия и поступления от источника новой заявки распределен по показательному закону. Следовательно, поток заявок от свободного источника является простейшим.

Поток с простым последействием является более общим по сравнению с простейшим потоком заявок. Простейший поток можно считать частным случаем потока с простым последействием, в том числе симметричного и примитивного потоков. С увеличением числа источников n и уменьшением параметра a последействие потока уменьшается. В предельном случае при n ® ¥ и a ® 0 так, что n a есть конечная величина и i принимает ограниченные значения, параметр потока l = n a не зависит от состояния системы, т.е. модель примитивного потока не переходит в модель простейшего потока заявок.