2015-02-18
2002
1. Если все значения признака уменьшить (увеличить) на одну и ту же величину А, то и средняя арифметическая уменьшится (увеличится) на ту же самую величину А:
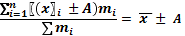
2. Если все значения признака разделить (умножить) на одну и ту же величину А, то и средняя арифметическая уменьшится (увеличится) в А раз.
3. Если вес каждого значения признака разделить на какое-либо постоянное число А, то средняя арифметическая не изменится.
ОБЩАЯ ТАБЛИЦА СРДЕНИХ
| Название формулы | Формула |
| Любая средняя величина |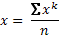 
|
| Средняя степенная |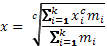 
|
| Средняя арифметическая простая |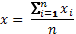 
|
| Средняя арифметическая взвешенная |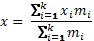 
|
| Средняя арифметическая хронологическая |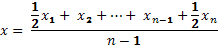 
|
| Средняя гармоническая простая |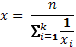 
|
| Средняя гармоническая взвешенная |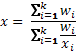 
|
| Средняя геометрическая простая | 
|
| Средняя геометрическая взвешенная | 
|
| Средняя квадратическая простая |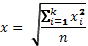 
|
| Средняя квадратическая взвешенная |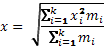 
|
| Мода для интервального ряда |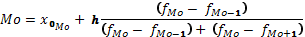 
|
| Медиана для интервального ряда |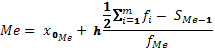 
|
xi – индивидуальное значение признака
|
|
|
n – количество единиц совокупности
mi – удельный вес
k – число вариантов
wi - ximi
Правило мажорантности средних: с увеличением показателя степени m увеличивается и соответствующая средняя величина: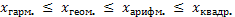 
ТЕМА 9
