Имеются следующие данные о производительности труда рабочих в двух бригадах:
Таблица 5.2
| Табельный номер рабочего | Произведено продукции за смену (штук) | |
| I бригада | II бригада | |
| Итого |
Определите показатели вариации.
Решение:
Для нашего примера размах вариации производительности труда для первой бригады составляет: R1 = 18 – 2 = 16; для второй бригады: R2 = 12 – 8 = 4.
Этот показатель прост в вычислении и указывает на общие размеры вариации, но он не даёт представления о степени колеблемости внутри совокупности, так как вычисляется на основе только двух крайних значений признаков совокупности.
Исчислим среднее линейное отклонение.
Порядок расчёта среднего линейного отклонения следующий:
1. по значениям признака исчисляется средняя арифметическая:
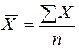 ;
;
2. определяются отклонения каждого варианта (Х) от средней:
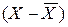 ;
;
3. рассчитывается сумма абсолютных отклонений:
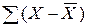 ;
;
4. сумма абсолютных отклонений делится на число значений:
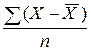 .
.
Произведя арифметические действия мы получим:
Таблица 5.3
| Табельный номер рабочего | I бригада | II бригада | ||||
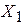 | 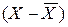 | 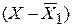 | 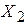 | 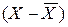 | 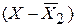 | |
| -8 -7 +2 +5 +8 | -2 -1 +1 +2 | |||||
| Итого: |
Тогда среднее линейное отклонение для I бригады составит: 30:5 = 6 шт., для II бригады – 6:5 = 1,2 шт.
Исчислим дисперсию.
Порядок расчёта дисперсии невзвешенной следующий:
1. определяется средняя арифметическая:
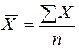 ;
;
2. рассчитываются отклонения вариант от средней:
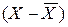 ;
;
3. возводятся в квадрат отклонения вариантов средней:
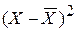 ;
;
4. суммируются квадраты отклонений:
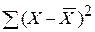 ;
;
5. полученная сумма делится на число вариант:
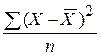 .
.
Произведя арифметические действия получим:
Таблица 5.4
| Табельный номер рабочего | I бригада | II бригада | ||||
| кол-во продукции (штук) | 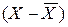 | 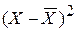 | кол-во продукции (штук) | 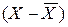 | 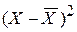 | |
| -8 -7 +2 +5 +8 | -2 -1 +1 +2 | |||||
| Итого: |
Тогда дисперсия для I бригады будет равна – 206:5 = 41,2 шт., а для II бригады – 10:5 = 2 шт.
Определяем среднее квадратическое отклонение по формуле:
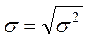 .
.
Тогда среднее квадратическое отклонение для I бригады будет равно 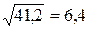 шт., а для II бригады
шт., а для II бригады 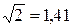 шт.
шт.
Определяем коэффициент вариации по формуле:
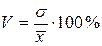 .
.
Тогда, для I бригады он будет равен 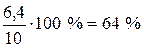 , а для II бригады
, а для II бригады 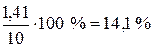 .
.
По величине коэффициента вариации можно судить о степени вариации признаков совокупностей. Чем больше его величина, тем больше разброс значений признаков вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя.
Если совокупность разбита на группы (или части) по изучаемому признаку, то для такой совокупности могут быть исчислены следующие виды дисперсии: групповые (частные), средняя из групповых (частных), межгрупповая.
Групповая (частная) дисперсия равна среднему квадрату отклонений отдельных значений признака внутри группы от средней арифметической этой группы (групповой средней). Она может быть исчислена как простая средняя или взвешенная соответственно по формулам:
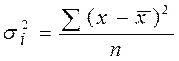 ,
, 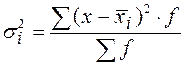 .
.
Эта дисперсия отражает вариацию признака только за счёт условий и причин, действующих внутри группы.
Средняя из групповых (частных) дисперсия – это средняя арифметическая, взвешенная из дисперсия групповых:
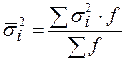 .
.
Межгрупповая дисперсия равна среднему квадрату отклонений групповых средних 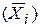 от общей средней
от общей средней 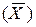 :
:
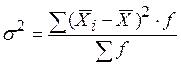 .
.
Межгрупповая дисперсия характеризует вариацию результативного признака за счёт группировочного признака.
Между указанными видами дисперсий существует определённое соотношение: общая дисперсия равна сумме средней из групповых дисперсий и межгрупповой дисперсии:
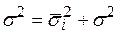 .
.
Это соотношение называют правилом сложения дисперсий. С его помощью, зная два вида дисперсий, можно определить третий:
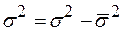
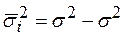
Поясним правило сложения дисперсий на примере.
 2015-02-18
2015-02-18 2777
2777








