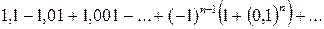 .
.
Решение. Первое условие признака Лейбница выполняется: 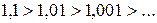 ; с другой стороны,
; с другой стороны, 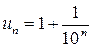 ,
, 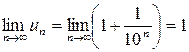 . Так как
. Так как 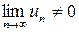 , то не выполнен необходимый признак сходимости ряда. Ряд расходится.
, то не выполнен необходимый признак сходимости ряда. Ряд расходится.
Пример 11. Исследовать сходимость ряда 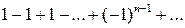 .
.
Решение. Общий член ряда не стремится к нулю, поэтому ряд расходится.
Пример 12. Исследовать сходимость ряда 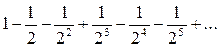 .
.
Решение. Составим ряд из абсолютных величин: 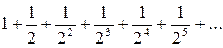 .
.
Этот ряд есть бесконечно убывающая геометрическая прогрессия и, следовательно, сходится. Значит, и данный ряд сходится, причем абсолютно.
Пример 13. Вычислить приближенно сумму ряда 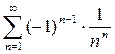 .
.
Решение. Данный ряд лейбницевского типа. Он сходится. Можно записать: 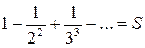 . Взяв пять членов, т.е. заменив S на
. Взяв пять членов, т.е. заменив S на
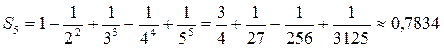 ,
,
сделаем ошибку, меньшую, чем 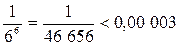 . Итак,
. Итак, 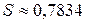 .
.
 2015-02-04
2015-02-04 1085
1085








