Контрольная работа для заочного отделения
Семестр.
Данко, П. Е. Высшая математика в упражнениях и задачах: в 2 ч. / П.Е. Данко, А. Г. Попов, Т. Я. Кожевникова. - 5-е изд., испр. - М.: Высшая школа.Ч.1.-1998.-304с.
Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа. -12-е издание. – СПб.: Лань, 2005.- 736 с
Б.М. Владимирский, А.Б. Горстко, Я.М. Ерусалимский. Математика: общий курс. – СПб.: Изд-во «Лань», 2002. – 954 с.
Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. — 5-е изд., стереотип. — М.: Наука, 1978. — 632с.
Демидович Б.П. Краткий курс высшей матетматики: Учебное пособие для вузов — M.: OOO «Издательство Астрель»: OOO «Издательство АСТ», 2001. — 656с.
Пискунов Н.С. Дифференциальные и интегральные исчисления: Учеб. для втузов. В 2-ч т. Т.II: — М.: Интеграл–Пресс, 2004. —544 с.
Введение.
Выполнять контрольную работу следует строго по графику. Каждый студент выполняет контрольную работу под вариантом, номер которого совпадает с его порядковым номером в групповом журнале. Решение задач нужно предоставить в письменном виде на отдельных листах (формата А 4, в скрепленном виде). Сдавать работу можно как в печатном, так и в письменном виде. Выполняя к.р., студент должен переписать условие соответствующей задачи, написать подробное решение, выделив ответ. Там, где это необходимо, дать краткие пояснения по ходу решения.
«ЧИСЛОВЫЕ и ФУНКЦИОНАЛЬНЫЕ РЯДЫ»
Числовые ряды. Достаточные признаки их сходимости
Пусть u 1, u 2, u 3, …, un, …, где un = f (n), –– бесконечная числовая последовательность. Выражение u 1 + u 2 + u 3 + … + un + … называется бесконечным числовым рядом, а числа u 1, u 2, u 3, …, un, … –– членами ряда; un = f (n) называется общим членом. Ряд часто записывают в виде 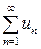 .
.
Сумму первых n членов числового ряда обозначают через Sn и называют n -й частичной суммой ряда:
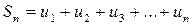 .
.
Ряд называется сходящимся, если его n -я частичная сумма Sn при неограниченном возрастании n стремится к конечному пределу, т.е. если 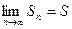 . Число S называют суммой ряда. Если же n -я частичная сумма ряда при
. Число S называют суммой ряда. Если же n -я частичная сумма ряда при 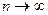 не стремится к конечному пределу, то ряд называют расходящимся.
не стремится к конечному пределу, то ряд называют расходящимся.
Ряд 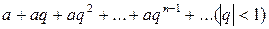 , составленный из членов любой убывающей геометрической прогрессии, является сходящимся и имеет сумму
, составленный из членов любой убывающей геометрической прогрессии, является сходящимся и имеет сумму 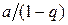 .
.
Ряд 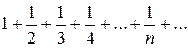 , называемый гармоническим, расходится.
, называемый гармоническим, расходится.
Необходимый признак сходимости. Если ряд 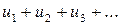 сходится, то
сходится, то 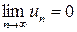 , т.е. при
, т.е. при 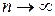 предел общего члена сходящегося ряда равен нулю.
предел общего члена сходящегося ряда равен нулю.
Таким образом, если 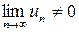 , то ряд расходится.
, то ряд расходится.
Перечислим важнейшие признаки сходимости и расходимости рядов с положительными членами.
Первый признак сравнения. Пусть даны два ряда
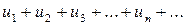 (1)
(1)
и
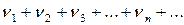 , (2)
, (2)
причем каждый член ряда (1) не превосходит соответствующего члена ряда (2), т.е. 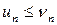
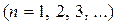 . Тогда если сходится ряд (2), то сходится и ряд (1); если расходится ряд (1), то расходится и ряд (2).
. Тогда если сходится ряд (2), то сходится и ряд (1); если расходится ряд (1), то расходится и ряд (2).
Этот признак остается в силе, если неравенства 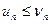 выполняются не при всех n, а лишь начиная с некоторого номера n = N.
выполняются не при всех n, а лишь начиная с некоторого номера n = N.
Второй признак сравнения. Если существует конечный отличный от нуля предел 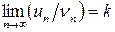 , то ряды
, то ряды 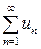 и
и 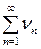 одновременно сходятся или расходятся.
одновременно сходятся или расходятся.
Радикальный признак Коши. Если для ряда 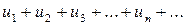
существует 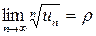 , то этот ряд сходится при
, то этот ряд сходится при 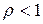 , расходится при
, расходится при 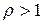 .
.
Признак Даламбера. Если для ряда 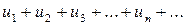 существует
существует 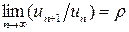 , то этот ряд сходится при
, то этот ряд сходится при 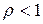 , расходится при
, расходится при 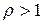 .
.
Интегральный признак Коши. Если f (x) при 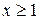 –– непрерывная положительная и монотонно убывающая функция, то ряд
–– непрерывная положительная и монотонно убывающая функция, то ряд 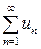 , где
, где 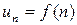 сходится или расходится в зависимости от того, сходится или расходится интеграл
сходится или расходится в зависимости от того, сходится или расходится интеграл 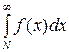
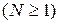 .
.
Рассмотрим теперь ряды, члены которых имеют чередующиеся знаки, т.е. ряды вида 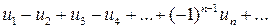 , где
, где 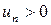
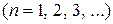 .
.
Признак сходимости знакочередующегося ряда (признак Лейбница). Знакочередующийся ряд сходится, если абсолютные величины его членов монотонно убывают, а общий член стремится к нулю. То есть, если выполняются следующие два условия: 1) 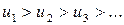 и 2)
и 2) 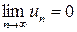 .
.
Возьмем n -ю частичную сумму сходящегося знакочередующегося ряда, для которого выполняется признак Лейбница:
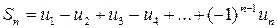 .
.
Пусть 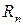 –– n -й остаток ряда. Его можно записать как разность между суммой ряда S и n -й частичной суммой Sn, т.е.
–– n -й остаток ряда. Его можно записать как разность между суммой ряда S и n -й частичной суммой Sn, т.е. 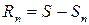 . Нетрудно видеть, что
. Нетрудно видеть, что
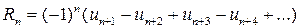 .
.
Величина 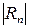 оценивается с помощью неравенства
оценивается с помощью неравенства 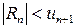 .
.
Остановимся теперь на некоторых свойствах знакопеременных рядов (т.е. знакочередующихся рядов и рядов с произвольным чередованием знаков своих членов).
Знакопеременный ряд 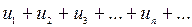 сходится, если сходится ряд
сходится, если сходится ряд 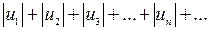 .
.
В этом случае исходный ряд 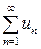 называется абсолютно сходящимся.
называется абсолютно сходящимся.
Сходящийся ряд 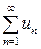 называется условно сходящимся, если ряд
называется условно сходящимся, если ряд 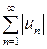 расходится.
расходится.
Пример 1. Исследовать сходимость ряда
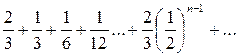 .
.
Решение. Данный ряд составлен из членов бесконечно убывающей геометрической прогрессии и поэтому сходится. Найдем его сумму. Здесь 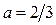 ,
, 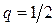 (знаменатель прогрессии). Следовательно,
(знаменатель прогрессии). Следовательно,
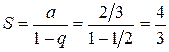 .
.
Пример 2. Исследовать сходимость ряда 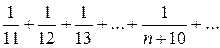 .
.
Решение. Данный ряд получен из гармонического отбрасыванием первых десяти членов. Следовательно, он расходится.
Пример 3. Исследовать сходимость ряда 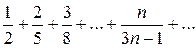 .
.
Решение. Так как 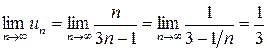 , т.е.
, т.е. 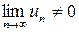 , то ряд расходится (не выполняется необходимый признак сходимости).
, то ряд расходится (не выполняется необходимый признак сходимости).
Пример 4. Исследовать сходимость ряда 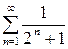 .
.
Решение. Члены данного ряда меньше соответствующих членов ряда 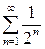 , т.е. ряда
, т.е. ряда 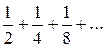 . Но последний ряд сходится как бесконечно убывающая геометрическая прогрессия. Следовательно, исходный ряд сходится.
. Но последний ряд сходится как бесконечно убывающая геометрическая прогрессия. Следовательно, исходный ряд сходится.
Пример 5. Исследовать сходимость ряда 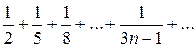 .
.
Решение. Сравним ряд с гармоническим рядом, у которого 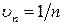 :
: 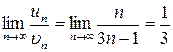 . Следовательно, данный ряд расходится.
. Следовательно, данный ряд расходится.
Пример 6. Исследовать сходимость ряда 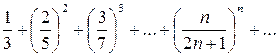 .
.
Решение. Здесь удобно применить радикальный признак Коши, поскольку 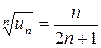 , а предел последней дроби находится просто:
, а предел последней дроби находится просто:
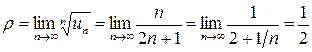 .
.
Так как 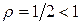 , то ряд сходится.
, то ряд сходится.
Пример 7. Исследовать сходимость ряда 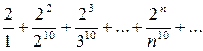 .
.
Решение. Применим признак Даламбера; имеем 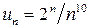 ,
, 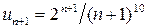 ,
, 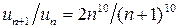 ; значит
; значит
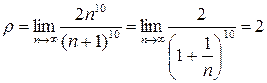 .
.
Так как 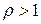 , то ряд расходится.
, то ряд расходится.
Пример 8. Исследовать сходимость ряда
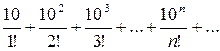 .
.
Решение. Имеем 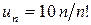 ,
, 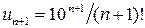 ,
, 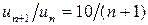 ,
, 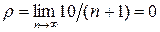 ,
, 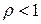 –– ряд сходится.
–– ряд сходится.
 2015-02-04
2015-02-04 5154
5154