Пример 26. Вычислить приближенно 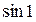 , сохранив в ряду четыре первых числа, и оценить погрешность.
, сохранив в ряду четыре первых числа, и оценить погрешность.
Решение. Воспользовавшись разложением
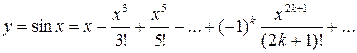 ,
,
где 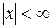 , запишем
, запишем
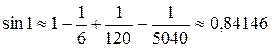 .
.
Ряд, составленный для 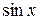 –– знакочередующийся, поэтому по признаку Лейбница погрешность не превосходит модуля первого члена из отброшенных, то есть
–– знакочередующийся, поэтому по признаку Лейбница погрешность не превосходит модуля первого члена из отброшенных, то есть 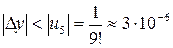 .
.
Таким образом, все пять знаков после запятой являются верными, погрешность 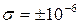 .
.
 2015-02-04
2015-02-04 793
793








