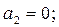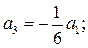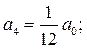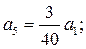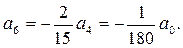2015-02-04
1149
Для приближенного интегрирования дифференциальных уравнений можно воспользоваться степенными рядами либо в виде ряда Маклорена
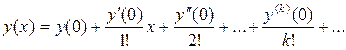, (13)
либо в виде ряда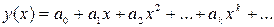 
(14)
с неопределенными коэффициентами.
При интегрировании нелинейных дифференциальных уравнений удобнее пользоваться рядом (13). Варианту (14) отдается предпочтение при интегрировании линейных дифференциальных уравнений.
Применение ряда Тейлора заключается в следующем. Записав решение дифференциального уравнения в виде ряда Тейлора, пользуемся самим уравнением и заданными начальными условиями для определения производных от искомой функции, которые затем подставляют в решение.
Пример 28. Найти частное решение дифференциального уравнения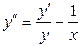 
, удовлетворяющее начальным условиям 
, 
.
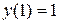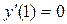Решение. Заданное дифференциальное уравнение является нелинейным и не относится к известным частным случаям, допускающеим понижения порядка заменой переменной. Воспользуемся для его интегрирования рядом Тейлора. Тогда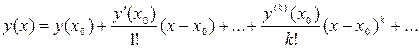 
.
Из начальных данных имеем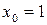 
, 
, 
.
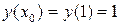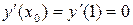Воспользовавшись дифференциальным уравнением, находим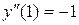 
.
Выполняя далее последовательное дифференцирование, получаем:
, 
;
, 
;
, 
….
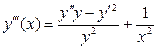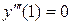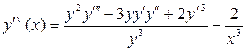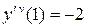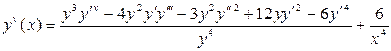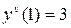Ограничившись первыми шестью членами ряда, запишем приближенное решение заданного уравнения в виде
.
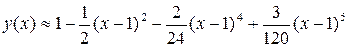Применяя степенной ряд с неопределенными коэффициентами, искомое решение и необходимые производные от него в виде рядов подставляют в уравнение, после чего приравнивают коэффициенты при одинаковых степенях x. При этом в процессе решения уравнения n -го порядка целесообразно первые n коэффициентов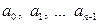 
выбрать в качестве параметров. Тогда сравнение коэффициентов позволит выразить все остальные коэффициенты 
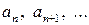, через 
.
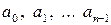Если заданы начальные условия, то через них определяются все коэффициенты ряда – решения. Остается подставить их и записать решение.
Пример 29. Записать в виде степенного ряда общее решение уравнения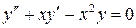 
, ограничившись первыми шестью членами.
Решение. Запишем решение в виде степенного ряда с неопределенными коэффициентами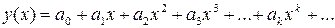 
.
Найдем первую и вторую производные:
,
.
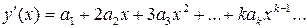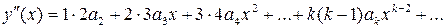Подставив полученные результаты в уравнение, получим
.
|
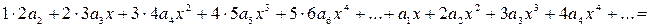
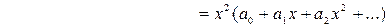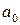и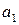 
в качестве параметров и воспользовавшись сравнением коэффициентов при одинаковых степенях x, находим при 
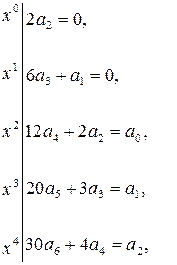
Итак, ограничившись первыми шестью членами ряда, записываем приближенное общее решение степенного ряда (14) с параметрам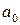и и :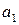
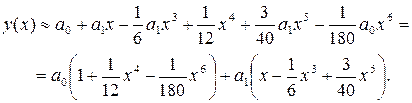
Очевидно, что такое представление решения заданного дифференциального уравнения справедливо в области сходимости полученного ряда.
