Приближенное вычисление определенных интегралов

Пример 27. Вычислить приближенно с точностью 0,001 значение функции Лапласа (интегральной функции нормального распределения случайных величин) 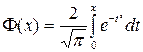в точке .

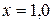Решение. В данном примере первообразная функция не вычисляется через элементарные, т.е. интеграл относится к категории «неберущихся».

Воспользовавшись разложением подинтегральной функции в степенной ряд, получим

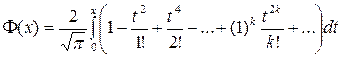
или после интегрирования

.

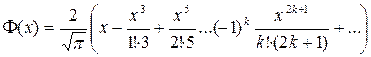Данная функция вычисляется с любой наперед заданной точностью при любом x, так как полученный ряд сходится на всей числовой оси.

При 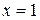получим

.

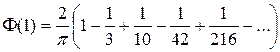Поскольку данный ряд –– знакочередующийся, то ошибка не превосходит модуля первого отброшенного члена, то есть

.

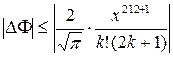Пр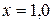и и 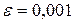должно выполниться условие

.

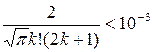Решая это неравенство методом проб, устанавливаем, что необходимое число членов в ряду 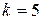, т.е.

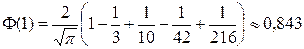
(табличное значение 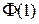с четырьмя верными знаками равно 0,8427).