2015-02-04
13247
Ряд называется функциональным, если его членами являются функции от некоторого аргумента x:
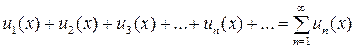. (3)
При конкретных значениях x, подставляемых в ряд (3), получаются различные числовые ряды, которые могут сходиться или расходиться. Совокупность всех значений x, при которых функциональный ряд (3) сходится, называется областью сходимости функционального ряда. Для некоторых x ряд может сходиться абсолютно, для некоторых условно. Поэтому различают также области абсолютной и условной сходимости функционального ряда.
При нахождении областей сходимости можно использовать все известные признаки сходимости. Как это делается, рассмотрим на конкретных примерах.
Пример 14. Найти область сходимости ряда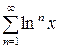 
.
Решение. Данный ряд представляет собой бесконечную геометрическую прогрессию со знаменателем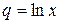 
. Так как прогрессия сходится лишь при 
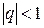, то данный ряд сходится, и притом абсолютно, при 
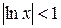, то есть 
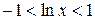, и, следовательно, неравенство 
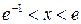определяет область сходимости исходного ряда.
Пример 15. Найти область сходимости ряда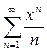 
.
Решение. При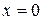 
сходимость ряда очевидна. Пусть 
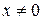. Применим признак Даламбера. И так как этот признак применим лишь для рядов с положительными членами, то исследуем ряд сразу на абсолютную сходимость. Здесь
; 
;
.
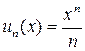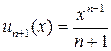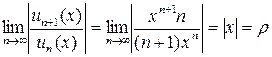Ряд сходится, и притом абсолютно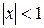, при 
. При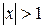 
ряд расходится. При 
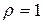признак Даламбера ответа не дает, и, следовательно, при 
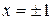ряд нужно исследовать особо. При 
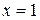получается гармонический ряд 
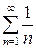, он расходится. При 
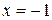получается сходящийся ряд Лейбница 
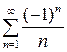. Таким образом, область сходимости данного ряда определяется неравенством 
.
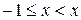Пример 16. Найти область сходимости ряда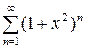 
.
Решение. Данный ряд –– бесконечная геометрическая прогрессия с знаменателем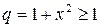 
. Следовательно, ряд расходится при всех действительных значениях x.
Пример 17. Найти область сходимости ряда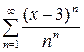 
.
Решение. Исследуем ряд на абсолютную сходимость с помощью радикального признака Каши. Здесь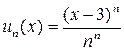 
;
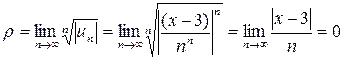при всех x.
Следовательно, ряд сходится абсолютно в бесконечном промежутке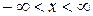 
. Этим неравенством и определяется область сходимости данного ряда.
Пример 18. Найти область сходимости ряда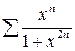 
.
Решение. Применяем признак Даламбера. У нас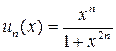 
; 
.
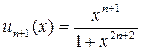Вычисляем
; 
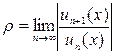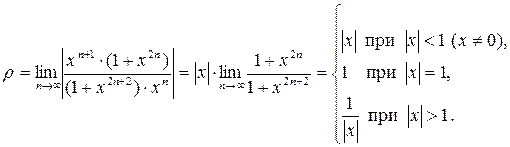
При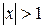
,
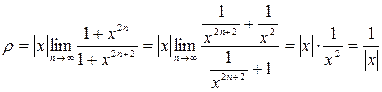так как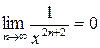 
.
При 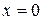сходимость ряда очевидна, то заключаем, что при всех 
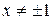ряд сходится, и притом абсолютно. При 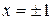получаются ряды вида 
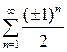, не удовлетворяющие необходимому признаку сходимости и, следовательно, расходящиеся. Таким образом, область сходимости данного ряда состоит из всех .
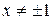Пример 19. Найти область сходимости ряда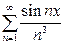 
.
Решение. При всех x справедливо неравенство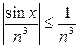 
. Ряд с общим членом 
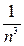сходится. Следовательно, данный функциональный ряд сходится абсолютно при всех x, согласно первому признаку сравнения.
