Ряд Тейлора для функции одной переменной. Всякая функция, бесконечно дифференцируемая в интервале 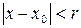 , т.е.
, т.е. 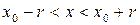 , может быть разложена в этом интервале в сходящийся к ней степенной ряд Тейлора
, может быть разложена в этом интервале в сходящийся к ней степенной ряд Тейлора
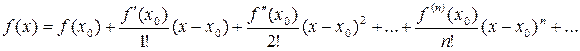 ,
,
если в этом интервале выполняется условие
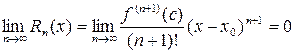 ,
,
где 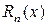 –– остаточный член формулы Тейлора (или остаток ряда),
–– остаточный член формулы Тейлора (или остаток ряда), 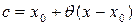 ,
, 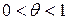 .
.
При 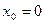 получается ряд Маклорена:
получается ряд Маклорена:
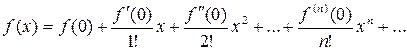 .
.
Если в некотором интервале, содержащем точку 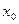 , при любом n выполняется неравенство
, при любом n выполняется неравенство 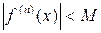 , где M –– положительная постоянная, то
, где M –– положительная постоянная, то 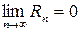 и функция
и функция 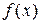 разложима в ряд Тейлора.
разложима в ряд Тейлора.
Приведем разложения в ряд Маклорена следующих функций:
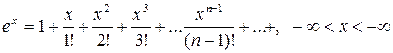 ; (4)
; (4)
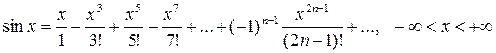 ; (5)
; (5)
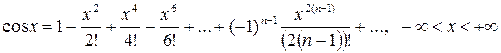 ; (6)
; (6)
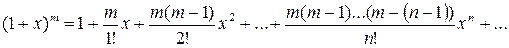 . (7)
. (7)
Это последнее разложение имеет место:
при 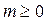 , если
, если 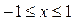 ;
;
при 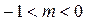 , если
, если 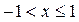 ;
;
при 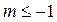 , если
, если 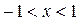 .
.
В частности при 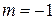 , получаем
, получаем
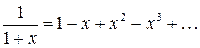 . (8)
. (8)
При 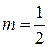 получаем
получаем
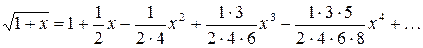 . (9)
. (9)
При 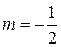 имеем:
имеем:
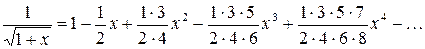 ; (10)
; (10)
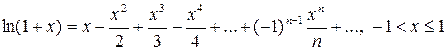 ; (11)
; (11)
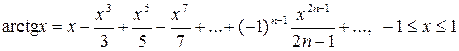 . (12)
. (12)
Пример 20. Разложить в ряд Маклорена функцию 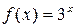 .
.
Решение. Так как 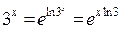 , то заменяя
, то заменяя 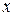 на
на 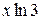 в разложении (4) получаем
в разложении (4) получаем
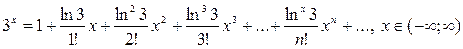 .
.
Пример 21. Записать ряд Маклорена функции для 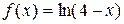 .
.
Решение. Так как 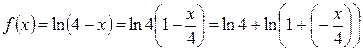 ,
,
то, воспользовавшись формулой (11), в которой заменим 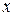 на
на 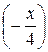 , получим
, получим
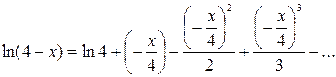 ,
,
или
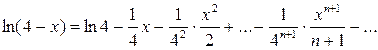 .
.
Ряд сходится, если
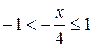 , т.е.
, т.е. 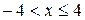 .
.
Пример 22. Разложить в ряд Маклорена функцию 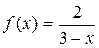 .
.
Решение. Воспользуемся формулой (8). Так как
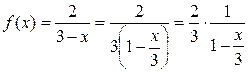 ,
,
то, заменив 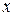 на
на 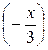 в формуле, получим
в формуле, получим
 ,
,
или
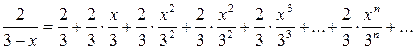 ,
,
где 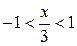 , т.е.
, т.е. 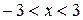 .
.
Пример 23. Разложить в ряд по степеням x функцию 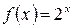 .
.
Решение. Найдем значения функции и ее производных при 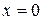 :
:
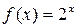 ,
, 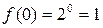 ,
,
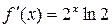 ,
, 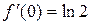 ,
,
 ,
, 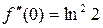
…………………………………..
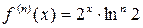 ;
; 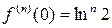 .
.
Так как 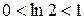 , то при фиксированном x имеет место неравенство
, то при фиксированном x имеет место неравенство 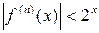 для любого n. Следовательно, функция может быть представлена в виде суммы ряда Маклорена:
для любого n. Следовательно, функция может быть представлена в виде суммы ряда Маклорена:
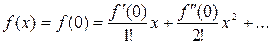 .
.
В данном случае 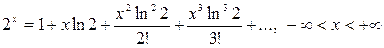 .
.
Это разложение можно получить и иначе: достаточно в разложении
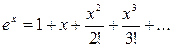
заменить 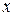 на
на 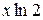 .
.
Пример 24. Разложить 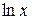 в ряд по степеням
в ряд по степеням 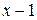 .
.
Решение. В разложении 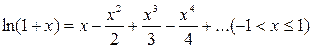 заменим
заменим 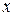 на
на 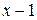 ; получим
; получим 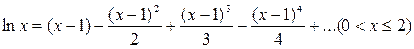 .
.
Пример 25. Разложить 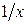 в ряд по степеням
в ряд по степеням 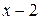 .
.
Решение. Воспользуемся равенством 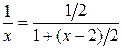 . Правую часть этого равенства можно рассматривать как сумму бесконечно убывающей геометрической прогрессии с первым членом
. Правую часть этого равенства можно рассматривать как сумму бесконечно убывающей геометрической прогрессии с первым членом 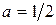 и знаменателем
и знаменателем 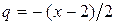 . Отсюда получаем
. Отсюда получаем
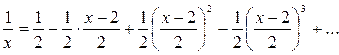 ,
,
т.е. 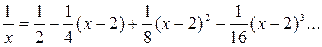 .
.
Так как 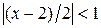 , то
, то 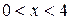 .
.
 2015-02-04
2015-02-04 2236
2236
