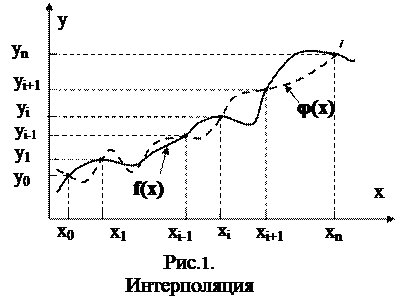II. Аппроксимация функций

1. Интерполирование -это аппроксимация (приближение) функции 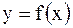с помощью алгебраического многочлена j(x) степени n, значения которого в заданных узлах 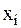(i=0,1,...,n) равны значениям функции в этих же узлах, т.е. j(x_i)=y_i=f(x_i), при этом полагается, что среди значений 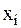нет одинаковых, т.е. x_i¹x_k при i¹k (Рис.1).

Многочлен j(x) называется интерполяционным и имеет вид:

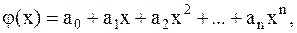(2.1)

Коэффициенты интерполяционного многочлена a_k (k=0,1,...n) определяются из системы линейных уравнений:

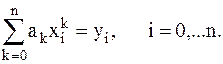(2.2)

Погрешность интерполяции R(x) определяется по формуле:

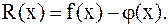(2.3)

2. Многочлены Лагранжа. При больших значениях n необходимо решать систему (2.2) из (n+1) уравнений, т.е. проводить большой объем вычислений. Как избежать этого? Это можно, например, сделать с помощью интерполяционных многочленов Лагранжа.

Рассмотрим многочлены степени n следующего вида, которые называются многочленами Лагранжа (выражения в угловых скобках учитывать не надо, они записаны для того, чтобы понять по какому принципу строятся эти многочлены):

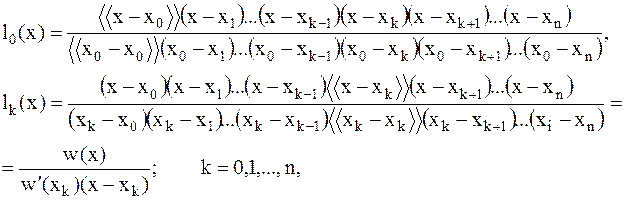(2.4)

здесь многочлен 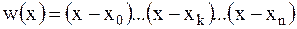имеет степень n+1 и он равен нулю во всех узлах x_k, k=0,1,2,…,n.

Можно видеть, что

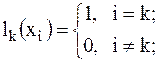(2.5)

т.е. многочлен Лагранжа l_k(x_i) равен нулю во всех узлах кроме k-го узла, а в самом k-ом узле он равен единице.

Используя это свойство, сразу можем сразу записать интерполяционный многочлен:

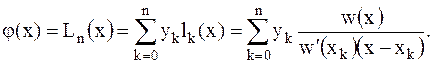(2.6)

Представление интерполяционного многочлена j(x) в таком виде называется обобщенным многочленом Лагранжа L_n(x) или просто интерполяционным многочленом Лагранжа.

На основании определения погрешности аппроксимации функции f(x) с помощью интерполяционного многочлена Лагранжа L_n(x) можем записать:

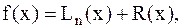(2.7)

при этом погрешность R(x) называется остаточным членом интерполяционного многочлена. Остаточный член, записанный в форме Лагранжа, имеет вид:

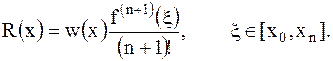(2.8)

3. Среднеквадратичное приближение. Коэффициенты интерполяционного многочлена j(x) определяются из системы линейных уравнений (2.2). При большом количестве узлов интерполяции (при больших значениях n) необходимо решать систему линейных уравнений большого порядка, что может привести к большим ошибкам. Применение обобщенного интерполяционного многочлена Лагранжа также ведет к большой относительной погрешности из-за накопления ошибок. Поэтому при больших значениях n используют иные приближения, например, среднеквадратичное приближение.

Среднеквадратичным приближением функций называется приближение, когда степень аппроксимирующего многочлена n меньше m (n<m), где m+1 равно количеству узлов 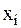(i=0,1,...,m). Случай m=n соответствует интерполяции.

Мерой отклонения многочлена 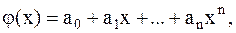от заданной функции y=f(x) при среднеквадратичном приближении является величина среднеквадратичного отклонения равная

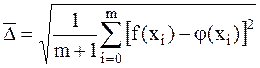. (2.9)

При построении аппроксимирующего многочлена j(x) нужно подобрать коэффициенты 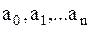так, чтобы величина 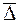была минимальной.

4. Метод наименьших квадратов. Так как 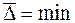, то 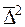достигает минимума при тех же значениях a_k, k=0,1,..,n. Введя обозначение y_i=f(x_i) рассмотрим функцию :

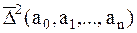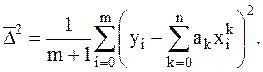(2.10)

Необходимым условием минимума функции 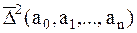является равенство нулю частных производных этой функции по переменным а_l, т.е.

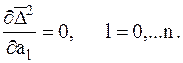(2.11)

Отсюда получаем:

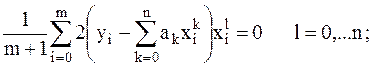(2.12)

или:

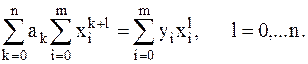(2.13)

Данная линейная система уравнений называется нормальной системой. Из решения этой системы уравнений определяются неизвестные коэффициенты a_k, при которых минимизируются среднеквадратичное отклонение между заданной функцией f(x) и аппроксимирующей функцией.

Варианты задания №3.

Используя интерполяционный многочлен Лагранжа вычислить в указанных точках значения функции y=f(x), заданной в виде таблицы, и оценить погрешность для заданного значения третьей производной:

1. x=0,8 и x=2,1;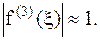

i	xi	yi
	0,5	5,1
	1,5	3,7
	2,5	4,3

2. x=0,7; x=1,1;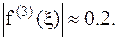

i	xi	yi
	0,4	0,1
	0,8	0,7
	1,2	0,3

3. x=1,8; x=3,1;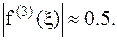

i	xi	yi
	1,5	2,2
	2,5	-0,7
	3,5	-4,3

4. x=0,18; x=0,21;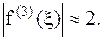

i	xi	yi
	0,1	0,1
	0,2	0,7
	0,3	0,3

5. x=0,1; x=0,2;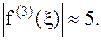

i	xi	yi
	0,05	-2,0
	0,15	-2,5
	0,25	-1,3

6. x=8; x=21;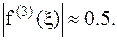

i	xi	yi
		0,1
		0,7
		0,3

7. x=0,25; x=0,9;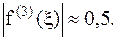

i	xi	yi
	0,1	3,1
	0,5	-0,7
	1,0	-3,3

8. x=0,28; x=0,31;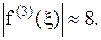

i	xi	yi
	0,1	-0,5
	0,2	-0,3
	0,3	-0,2

9. x=0,8; x=2,1;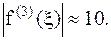

i	xi	yi
	0,0	15,0
	1,5	17,0
	3,0	9,5

10. x=1,8; x=1,75;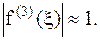

i	xi	yi
	1,0	-0,1
	1,5	1,7
	2,0	8,7

11. x=0,8; x=2,1;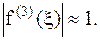

i	xi	yi
	0,5	0,1
	1,5	-0,7
	2,5	-0,3

12. x=0,7; x=1,1;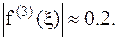

i	xi	yi
	0,4	0,15
	0,8	0,4
	1,2	0,3

13. x=1,8; x=3,1;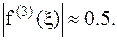

i	xi	yi
	1,5	1,2
	2,5	-0,7
	3,5	-0,3

14. x=2,5; x=1,5;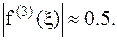

i	xi	yi
	1,1	4,4
	2,2	-1,7
	3,3	-3,4

15. x=0,1; x=0,2;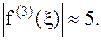

i	xi	yi
	0,05	-1,0
	0,15	-2,1
	0,25	-1,4

16. x=8; x=21;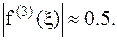

i	xi	yi
		0,15
		0,47
		0,43

17. x=0,25; x=0,9;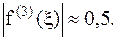

i	xi	yi
	0,1	2,1
	0,5	-0,5
	1,0	-2,3

18. x=0,28; x=0,31;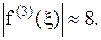

i	xi	yi
	0,1	-0,3
	0,2	0,3
	0,3	-0,1

19. x=0,8; x=2,1;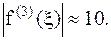

i	xi	yi
	0,0	10,0
	1,5	7,0
	3,0	5,5

20. x=1,8; x=1,75;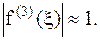

i	xi	yi
	1,0	-0,1
	1,5	1,7
	2,0	8,7

21. x=0,4 и x=3,5;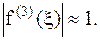

i	xi	yi
	0,5	-0,5
	1,5	0,7
	2,5	0,3

22. x=0,4; x=0,6;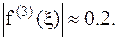

i	xi	yi
	0,0	0,1
	0,8	0,3
	1,6	0,3

23. x=0,4; x=2,3;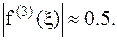

i	xi	yi
	3,5	0,2
	6,5	0,5
	9,5	-0,9

24. x=0,8; x=1,4;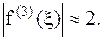

i	xi	yi
	0,1	-0,5
	0,7	0,7
	1,3	0,3

25. x=0,5; x=1,2;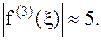

i	xi	yi
	0,05	-22,0
	0,25	3,5
	0,45	-8,3

26. x=6; x=13;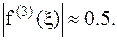

i	xi	yi
		-0,7
		0,4
		-0,9

27. x=0,12; x=1,5;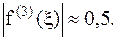

i	xi	yi
	0,1	-7,5
	1,5	-0,67
	2,0	7,3

28. x=0,8; x=0,98;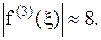

i	xi	yi
	0,1	0,5
	0,5	-3,3
	0,9	-0,7

29. x=0,38; x=2,1;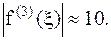

i	xi	yi
	0,0	1,0
	0,5	-1,7
	1,0	-0,5

30. x=1,3; x=2,1;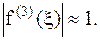

i	xi	yi
	1,0	-0,5
	3,5	-2,2
	6,0	-0,6

31. x=0,4; x=2,3;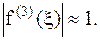

i	xi	yi
	0,0	-0,1
	1,5	0,7
	3,0	0,4

32. x=0,3; x=0,5;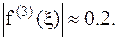

i	xi	yi
	0,6	-1,5
	1,8	-0,3
	3,0	0,8

33. x=1,5; x=2,7;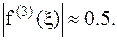

i	xi	yi
	0,5	-1,2
	2,5	-0,4
	4,5	0,1

34. x=2,1; x=1,1;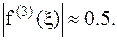

i	xi	yi
	0,3	0,9
	1,2	-1,3
	2,1	1,4

35. x=0,3; x=1,2;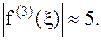

i	xi	yi
	10,5	6,0
	15,5	-0,4
	20,5	-3,6

36. x=8; x=21;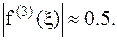

i	xi	yi
		0,15
		0,47
		0,43

37. x=0,2; x=1,9;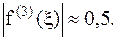

i	xi	yi
	0,1	-2,1
	0,8	-6,5
	1,5	-0,3

38. x=0,4; x=2,5;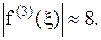

i	xi	yi
	0,15	40,0
	2,25	-34,3
	3,35	-20,7

39. x=0,6; x=3,3;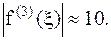

i	xi	yi
	0,0	-1,4
	3,5	-3,5
	7,0	-2,5

40. x=0,41; x=0,75;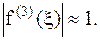

i	xi	yi
	1,3	0,8
	2,5	-3,7
	3,7	-0,5